SYM:簡明理解零知識證明歷史、原理與發展現狀_NAR幣

原文標題：《零知識證明最簡介紹：歷史、原理、實現》

密碼學可以說是區塊鏈技術的基石，而其中的零知識證明更是因為深度契合區塊鏈的技術特點，而得到了廣泛的應用和關注。

本文旨在用最簡單的語言和形式，向大家介紹零知識證明相關的歷史、概念、原理、技術實現以及發展現狀。

那么讓我們開始吧。

密碼學是一門可以追溯到 2000 多年前的古老學問，其發展歷史主要可以劃分為以下幾個階段：

這一時期的密碼學主要被應用于軍事領域，如何有效的傳遞密文，又能防止被敵人截獲后破解，是其主要考量。16 世紀由法國人發明的「維吉尼亞密碼」是古典密碼理論發展上的一個重要里程碑，它使用一個詞組作為密鑰，詞組中每一個字母都將確定一個替換表，「維吉尼亞密碼」循環的使用每一個替換表完成明文字母到密文字母的變化。

明文：ilovebitcoin

密鑰：satoshi

對于第一個字母 i，取第 i 行第 s 列，得到 A；第二個字母 l，取第 l 行第 a 列，得到 L…依次循環，最后得到密文：ALHJWIQLCHWF。可見，在不知道密鑰的前提下，不借助計算機已經非常難以破解這樣的密碼。

這一階段真正的開始源于香農在 20 世紀 40 年代末發表的一系列論文，特別是 1949 年的「Communication Theory of Secrecy Systems （保密系統通信理論）」，把已有數千年歷史的密碼學推向了基于信息論的科學軌道，密碼學終于從藝術轉向科學。

這一時期的重要突破是 DES 的出現，直至今日也只能用窮舉法對其進行破解。DES 加密算法風行世界，并在金融等商業領域得到了廣泛的應用。

1977 年，麻省理工學院的 Ron Rivest、Adi Shamir、Leonard Adleman 提出的非對稱加密算法 RSA，有效的解決了密鑰傳送的問題，標志著密碼學進入了百家爭鳴的現代階段。

26.94億枚ARB于2日前轉移至約140個EOA地址，本應有4年鎖倉期限制:4月3日消息，據Lookonchain數據顯示，26.94億枚ARB于2日前通過0x1e70開頭地址被轉移分配至約140個EOA地址，該數量的ARB應該是分配給OffchainLabs團隊、未來團隊和顧問的部分（26.94%），但該部分Token應該有4年的鎖倉期。

Lookonchain補充表示，0x8d45開頭地址在收到ARB后已將2256萬枚ARB（約合2800萬美元）轉移至Coinbase。其他地址雖然還沒有轉賬操作，但收到的ARB可以隨時轉入交易平臺出售，不受代碼限制。注：據Arbitrum官方于3月16日發布的Medium文章《ARBITRUM: THE NEXT PHASE OF DECENTRALIZATION》內容顯示，所有投資者和團隊Token（共計54.47%）都將有4年的鎖倉期，首次解鎖發生在一年內，然后在剩余三年內每月線性解鎖。[2023/4/3 13:41:15]

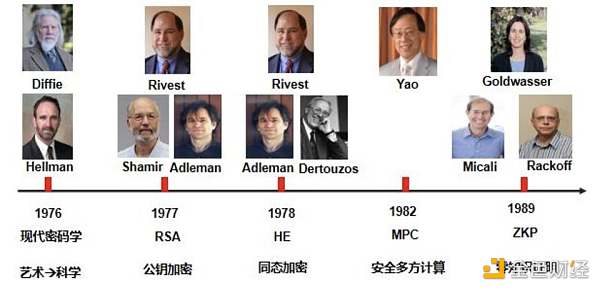
1989 年，由麻省理工學院研究人員 Goldwasser、Micali 及 Rackoff 提出了「零知識證明」的概念，當時的他們一定不曾想到，若干年后出現的區塊鏈技術徹底激活了零知識證明的應用，而零知識證明則為區塊鏈技術提供了一種絕佳的解決方案。零知識證明的方法特點和區塊鏈技術的系統特點達成了完美的契合。

零知識證明是指，在不揭曉我所知道或擁有的某樣東西的前提下，向別人證明我有很大概率確實知道或擁有這樣東西。

zkSNARK 則是在區塊鏈中應用最廣泛的一種零知識證明，其全稱是「zero-knowledge Succinct Non-Interactive Arguments of Knowledge （簡潔非交互式零知識證明）」。

光聽定義，大家一定一頭霧水，本節將借用一個例子，盡可能接地氣的向大家介紹這兩個概念。

法院駁回了對MicroStrategy的稅務欺詐指控:金色財經報道，哥倫比亞特區高等法院駁回了針對美國商業情報公司 MicroStrategy 的民事訴訟，該訴訟指控該公司幫助其聯合創始人邁克爾塞勒 (Michael Saylor) 逃避所得稅支付。根據最近的一份文件，Saylor 和 MicroStrategy 在 10 月份提出了駁回申訴的動議，法院于 2 月 28 日裁定支持該請求。據悉，該案件是 DC 剛剛修訂的虛假申報法案下的第一起案件，要求支付高達 2500 萬美元的所欠所得稅和未公開金額的三倍損害賠償、民事處罰和其他救濟。

此前消息，Saylor被指控住在佛羅里達州，但其中有183天居住在華盛頓特區。他獲得了駕照，并在佛羅里達州登記投票，假裝是那里的居民，以此來逃避稅款。[2023/3/4 12:41:40]

Alice、Bob 和 Charlie 都是數獨愛好者，所謂數獨是這樣一種游戲，玩家需要根據 9×9 盤面上的已知數字，推理出所有剩余空格的數字，并滿足每一行、每一列、每一個粗線宮（3x3）的數字均含 1 到 9，且不重復。

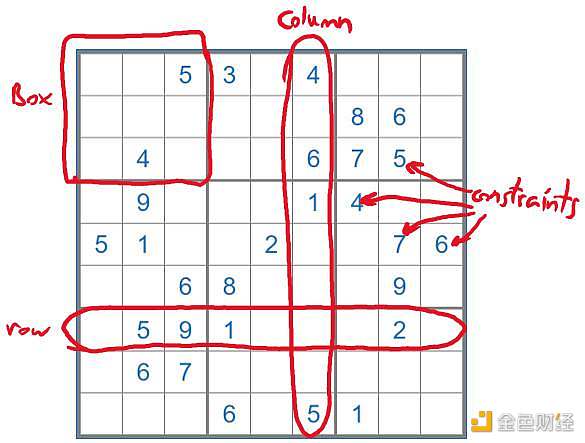
有一天 Alice 設計了一道巨難的數獨題目來考 Bob 和 Charlie，Bob 苦思冥想了幾天也做不出，便向 Alice 抱怨這肯定是道無解的題目。Alice 不想將實際的解告訴 Bob，但是又需要證明她確實知道解，于是她設計了一種巧妙的「零知識證明」的方式。

證明（The Proof )

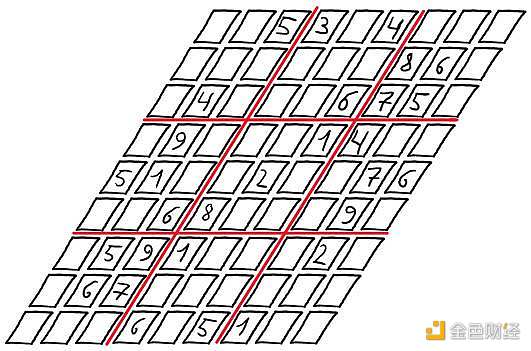
Alice 拿出 81 （9x9）張空白的卡片，并在每張紙上寫上 1-9 中的一個數字，接著她將代表謎面的卡片數字面朝上、代表謎底的卡片數字面朝下都放在桌上，并組成了 9x9 的矩陣。

Uniswap更改社區治理流程的提案已投票通過:12月22日消息，Uniswap基金會發起的更改社區治理流程的提案投票已結束，贊成率近100%。

新提案提議將為期七天的“征求意見”（RFC）流程取代原有為期三天的共識檢查流程。此外，Temperature Check的投票法定人數要求將增加至1000萬UNI。[2022/12/22 22:00:02]

隨機挑戰（The Random Challenge）

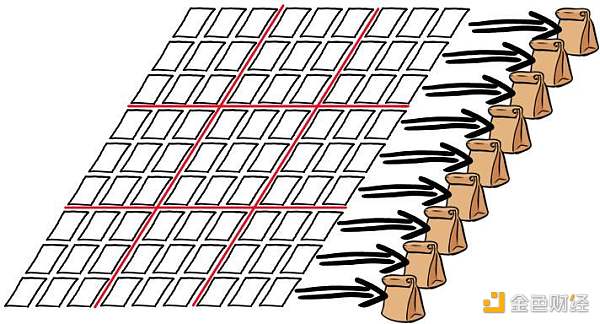
接下來怎么讓 Bob 確認這就是正確的解呢？很簡單，由 Bob 隨機選擇行、列或是粗線宮中的一種進行驗證，假如選擇行，則將這 81 張卡片按 9 行分別放到 9 個麻布袋中，搖勻并確保卡片次序打亂。

驗證（The Verify）

簡潔（Succinct）

雖然數獨游戲有 3 種情況需要驗證（行、列、粗線宮），但每次驗證時 Bob 實際只需要驗證其中的一種，這有效減少了驗證工作量，提供給驗證者的實際是一個比原命題小的多的證明，這就是所謂的簡潔。

重復（Repeat）

之后重復這個隨機驗證步驟，我們假設 Alice 運氣很好，每次都能提前猜中 Bob 會選擇哪種驗證方式，并以此來模擬一個解，那么她通過 1 次驗證的概率為 1/3，通過 2 次驗證的概率為 1/9，通過 10 次驗證概率就只有 1/59049 了。在不厭其煩的進行了 20 次驗證之后，Bob 無奈的承認，Alice 是真的知道這個答案的解，因為 Alice 憑運氣通過驗證的概率只有 35 億分之一！（這也是為何我們說零知識證明是在概率上成立的證明）

一位加密交易員通過操縱GMX上AVAX代幣價格獲利超過50萬美元:金色財經報道，一位加密貨幣交易員部署了數百萬美元來操縱去中心化交易所GMX 上 Avalanche的AVAX代幣的價格，通過利用基本漏洞的策略獲利超過 50萬美元。在周日的幾條推文中，Genesis Trading衍生品負責人Joshua Lim表示，該交易員利用GMX漏洞大約五次，總利潤超過 500,000 美元至 700,000 美元。安全公司 PeckShield 在周日早上的一條推文中也將收益定為 565,000 美元，該推文已被刪除。

Lim 說，這位交易員每次的頭寸在 400 萬到 500 萬美元之間，并在他們進行的第一筆交易中提取了超過 158,000 美元。他補充說，這不是典型的漏洞利用，因為 GMX “按設計”工作。

金色財經此前報道，GMX稱，監測到AVAX/USD價格被故意操縱。[2022/9/19 7:06:31]

模擬（The Simulation）

這個時候，Charlie 也來向 Alice 抱怨這個題目的無解，Alice 和 Bob 又重復了剛才的證明，沒想到卻沒有得到 Charlie 的認可。Charlie 提出了這個證明中的漏洞，如果 Bob 和 Alice 是一伙的，每次 Bob 都會提前告訴 Alice 他要選擇的驗證方式，那么 Alice 就可以很容易的在沒有解的情況下模擬出一個證明來通過這些測試。

非交互式證明（Non-Interactive Proofs）

不可能讓每個持有這種懷疑的人都重復一遍 Bob 進行的隨機驗證，于是三個小伙伴設計了一臺神奇的機器，Alice 只需要提交一次卡片，這臺機器就可以按照初始設置好的驗證序列，自動化的對這些卡片進行重復驗證。驗證從交互式的，變成了非交互式的。這里我們要注意，并不是說非交互式證明就沒有重復隨機實驗這個過程。實際上，只不過是隨機點不由驗證者給出，而是由一個可信的第三方在初始化階段就給出，這樣一來，證明者就可以直接給出證明，驗證者只需要驗證證明即可，驗證者和證明者之間不再需要交互。

Blockchain.com CEO：加密市場還將面臨更多困境，但最終有助于鞏固加密經濟:金色財經消息，Blockchain.com首席執行官Peter Smith表示，“創造性破壞”最終有助于鞏固加密經濟，在最近的市場波動之后，仍有較弱的協議、資產和投資者會面臨困境。

Smith表示，更多的痛苦即將到來，更多的風險將暴露出來，但最終，這對去中心化經濟來說是一件好事，因為這將是一個漫長的采用和發展過程。（CNBC）[2022/5/20 3:29:36]

可信設置儀式（Trusted Setup Ceremony）

其中最有趣也最重要的環節就是驗證序列的初始設置。在機器啟動前，會有一排設置旋鈕，通過這些旋鈕可以選定每一輪的驗證方式。在設置這些旋鈕時，每個人依次進入放置機器的房間，選擇一個旋鈕并設置好，之后就用一個鐵盒子徹底焊死這個旋鈕，讓其他人無法看見也無法改變這個旋鈕的選擇。為了讓初始設置盡可能的可信，小伙伴們邀請了鎮長、小學校長和警察局長這三位小鎮上最德高望重的長者來參加設置儀式，大家都相信他們絕對不可能參與作假，因此他們稱之為「可信任的初始設置儀式」。

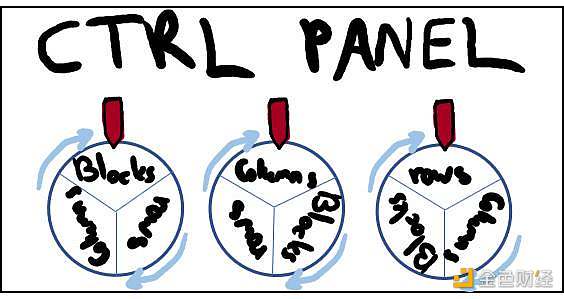
一臺數獨游戲的簡潔非交互式零知識證明機，誕生了！

通過上一節我們已經弄明白了零知識證明和 zkSNARK 的基本概念和原理，這一節我們再來一窺 zkSNARK 的技術實現。可以說整個實現過程相當的繁瑣晦澀，且需要一定的背景知識，因此本小節只力圖講清楚其核心思想，而不拘泥于過分復雜的數學推導。

我們從一個方程式開始，X^3 + X + 5 = 35，顯然解是 3。那么現在，證明者如何向驗證者證明自己知道方程的解是 3，而又不告訴驗證者這個解呢？

首先，我們將方程轉化為計算機語言，這很容易實現：

y = x*3return x + y + 5

接著，我們將上面的代碼拍平。所謂將代碼拍平，是指讓代碼一次只做一件事，形如 x = y op z。

拍平后，代碼變成以下語句：

sym_1 = x * xy = sym_1 * xsym_2 = y + x~out = sym2 + 5

然后，我們引入 R1CS 一階約束系統（rank-1 constraint system），R1CS 是一個由三向量組（a, b, c）組成的序列，同時有一個解向量 s，s 滿足 s·a * s·b - s·c = 0。

在本例中，s 的結構為（~one\, x\, ~out\, sym_1\, y\, sym_2），可見其由一個特殊的 ~one、方程的解 x、方程的輸出 ~out 和一系列中間變量（拍平后的語句等號左邊的變量）構成，其順序不重要，只要保證有序即可。

我們把語句變換成如下形式，來方便我們求解 abc：

x * x - sym_1 = 0sym_1 * x - y = 0y + x - sym_2 = 0sym_2 + 5 - ~out = 0

我們很容易得出第一個式子對應的三個向量：

a = [0, 1, 0, 0, 0, 0]b = [0, 1, 0, 0, 0, 0]c = [0, 0, 0, 1, 0, 0]

推導過程其實很簡單，我們知道要滿足 s·a * s·b - s·c = 0，那么對應第一個式子 x * x - sym_1 = 0，只需要 s·a = x、s·b = x、s·c = sym_1 即可，而 s =（~one\, x\, ~out\, sym_1\, y\, sym_2），那么 a 只要在 x 的位置等于 1，其余位置等于 0，即得出（0，1，0，0，0，0）。

大家可能對上面一系列眼花繚亂的變換感到莫名其妙，我們究竟在做什么？這里要揭曉謎底了，我們對每個式子驗證 s·a * s·b - s·c = 0，其本質是在驗證每一步都得到了正確的計算，也即如果我們可以驗證每一步都是正確的，那么最終結果也一定是正確的。

以上的每一步，看似都在舍近求遠，因為 s 里本身就包含了方程的解 x，驗證者只需把 x 代入就能進行驗證。但從另一個角度看，通過這一系列的轉換，我們構建了一種將證明和驗證分離的方式。在證明過程中，證明者需要知道解并生成一系列中間結果，而驗證者則只需要驗證其一系列結果構成的解向量是否滿足一系列約束，而不需要關心這個解到底是多少。

現在只剩一個問題留待解決，就是能否通過一種方式，讓驗證者看不到裸著的解 x，同時依然可以進行驗證過程。答案是肯定的，借由橢圓曲線、雙線性對運算和指數知識假設這一系列數學手段我們就可以做到這一點，因為其推導過程過于復雜，本文不做贅述。整個 zkSNARK 的技術實現流程參見下圖，需要了解更多細節的同學可以閱讀參考資料中給出的 Vitalik 的文章。

零知識證明目前有如下幾種協議，每個協議代表一條實現零知識證明的道路，不同道路最后會產生不一樣的效果。

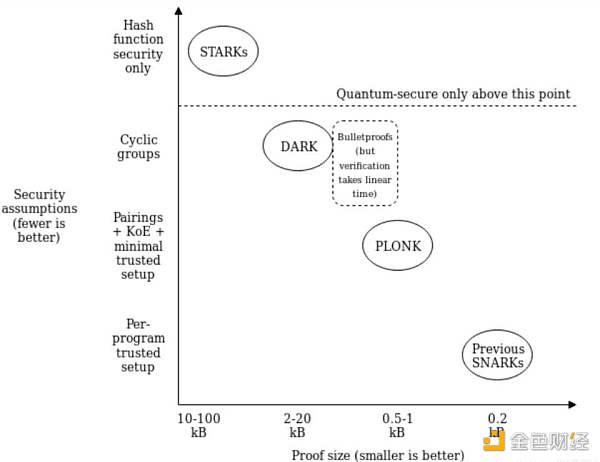
其中，安全性最高的是 STARKs 算法，其不依賴數學難題假設，具有抗量子性，并實現了透明通用字符串；Proof size 最小的 snarks 協議是 groth16 算法；Plonk 是 SNARK 協議中的一個算法，Proof size 和安全性處于適中狀態。

作為區塊鏈技術中應用最廣泛的 SNARKs，已經發展出了諸多各具特點的協議算法：

Groth16：Groth16 是目前最快、數據量最小的 zk-SNARK，被用于 Zcash 等。Groth16 的 CRS （the Common Reference String）不是通用的，其設置需要綁定到一個特定的電路。由于其速度和證明的小數據量，因此常常被新的 zk-SNARK 拿來比較性能。

Groth16 論文鏈接

Sonic：Sonic 是一種早期的通用 zk-SNARK 協議，支持通用、可升級的參考字符串，論文發表于 2019 年 1 月。Sonic 的證明大小固定，但是驗證成本高，理論上可以將多個證明分批驗證以獲得更好的性能。下面列舉的許多新的 zk-SNARK 都是基于 Sonic。

Sonic 論文鏈接

Fractal：Fractal 是一種允許遞歸的 zk-SNARK。通過對電路的預處理實現了透明設置。證明最大 250KB，這比其他構建生成的證明都要大的多。

Fractal 論文鏈接

Halo：Halo 支持遞歸證據組織，無需可信設置，與其他新的 zk-SNARK 構建不同，Halo 的驗證時間是線性的。

Halo 論文鏈接

SuperSonic：Sonic 的改進版，是第一個在驗證時間和證明數據量方面實用化的透明 zk-SNARK。

SuperSonic 論文鏈接

Marlin：Sonic 的改進版，證明時間縮短 10 倍，驗證時間縮短 4 倍。

Marlin 論文鏈接

Plonk：Sonic 的改進版，證明時間縮短 5 倍。

Plonk 論文鏈接

當前零知識證明缺乏專用硬件，導致硬件成本偏高，租用云服務器滿負荷下成本約為 0.002 元 / 筆，有空載情況下約為 0.02 元 / 筆。Vitalik 曾提出一個設想，當以太坊共識機制改為 PoS，不需要那么多挖礦硬件后，這些算力可以經改造后轉向支持零知識證明，這可能有效降低零知識證明的運行成本。

如今，零知識證明已經在區塊鏈領域大放異彩，包括第一個實現 zkSNARK 的匿名加密貨幣 Zcash （ZEC）、Layer2 的主要解決方案 zk Rollup 等等。

DeGate 團隊也將在產品實現中大量應用零知識證明，藉由其強大特性，我們將 Orderbook 的撮合交易轉到 MatchNode （Layer3）中進行，使用戶可以實時的掛單、撤單和成交，且其中掛單撤單免費；之后再將訂單批量結果生成證明，傳回 Layer2 上進行驗證，這讓 DeGate 在繼承以太坊安全性的同時，既可以隱藏下單關鍵信息又可以有效降低 Layer2 上的 Gas 費消耗。而我們的最終目標是，無論在操作體驗上，還是手續費消耗上，都使 DeGate 達到媲美中心化交易所的水平。

Tags：ALINARARKSYMNeuralink V2NAR幣Dark.BuildSymVerse

fil幣價格今日行情