CRO:Scroll 創始人張燁：zkEVM 設計，優化和應用_Escrowed Illuvium

原文作者：YeZhang

原文來源：ScrollCN

編譯：F.F

在最新的ZKPMooc課程中，Scroll的聯合創始人張燁發表了關于zkEVM設計，優化和應用的演講。Scroll在構建以太坊等效的ZK-Rollup，在字節碼級別的兼容，直接支持所有現有的工具。

以下是視頻的聽錄文字版本

演講分成四個部分，第一部分張燁介紹了開發背景以及我們為什么首先需要zkEVM以及為什么它在最近兩年間變得如此受歡迎，第二部分通過一個完整的流程，講解如何從頭開始構建zkEVM包括算術化和證明系統，第三部分通過一些有趣的研究問題來談論了Scroll在構建zkEVM時遇到的問題，最后介紹了一些其他使用zkEVM的應用。

背景和動機

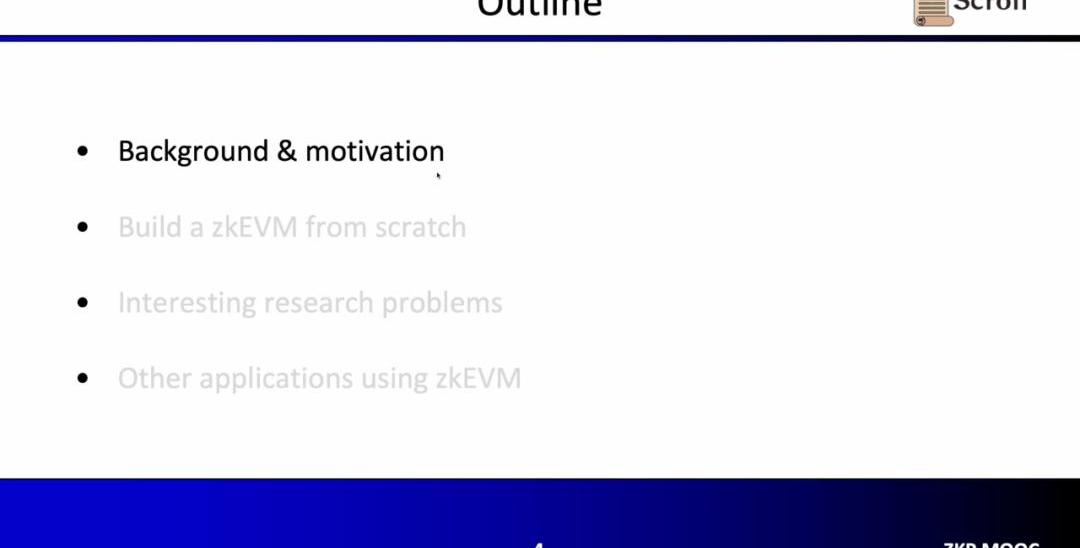
傳統的Layer1區塊鏈會有一些節點通過P2P網絡共同維護。他們在收到用戶的交易時，會在EVM的虛擬機內執行，讀取調用合約和存儲，并依照交易更新全局的狀態樹。

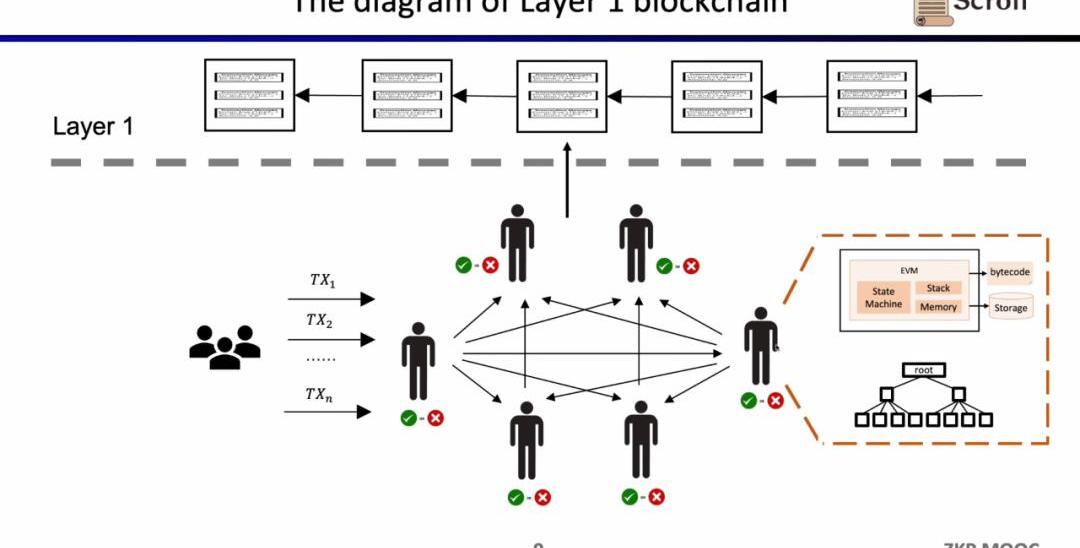
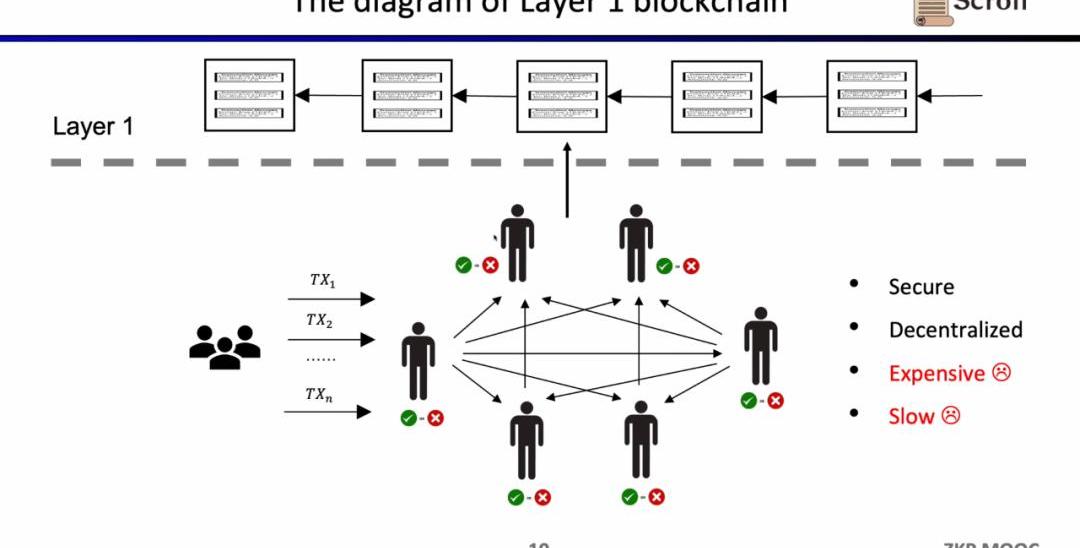
這樣的架構的優勢在于去中心化和安全性，缺陷就是在L1上的交易手續費昂貴，并且交易確認緩慢。

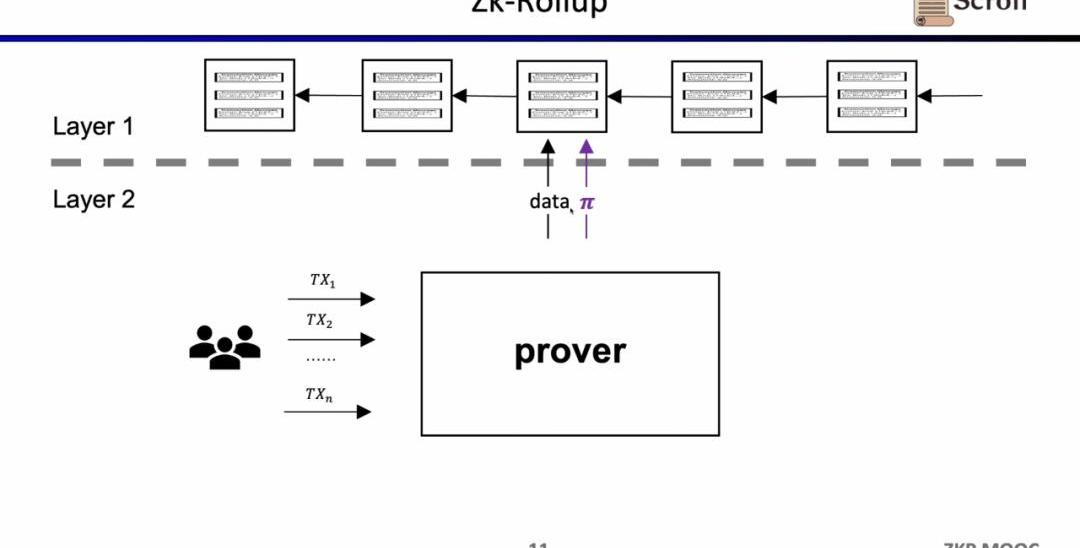
ZK-Rollup的架構中，L2網絡只需將數據和驗證數據正確性的證明上傳至L1，其中證明通過零知識證明電路計算而來。

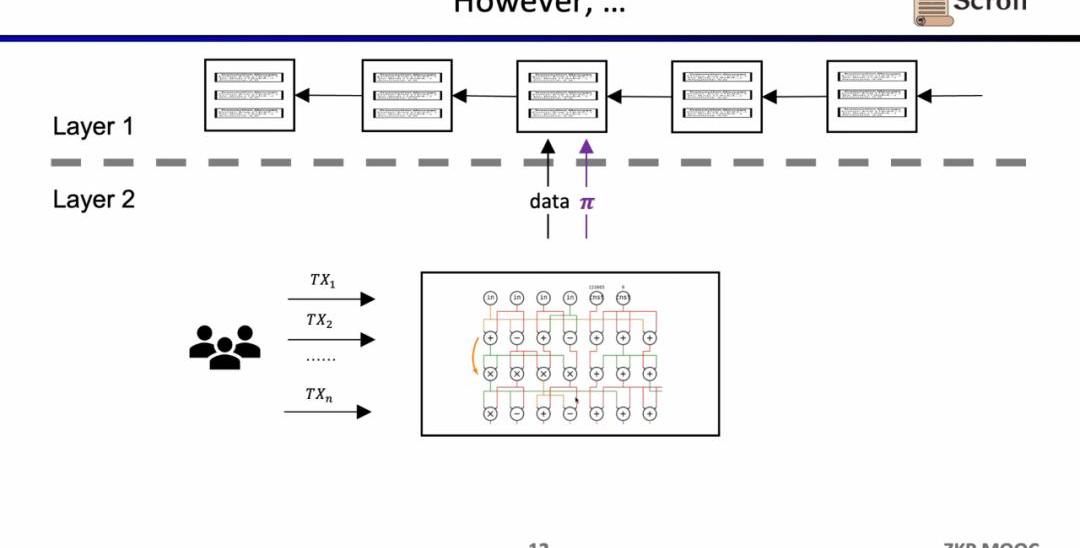
在早期的ZK-Rollup中，電路是針對特定應用而設計，用戶需要將交易發送給不同的證明者，然后不同應用的ZK-Rollup再將自己的數據和證明提交至L1。這樣帶來的問題是，喪失了原先L1合約的可組合性。

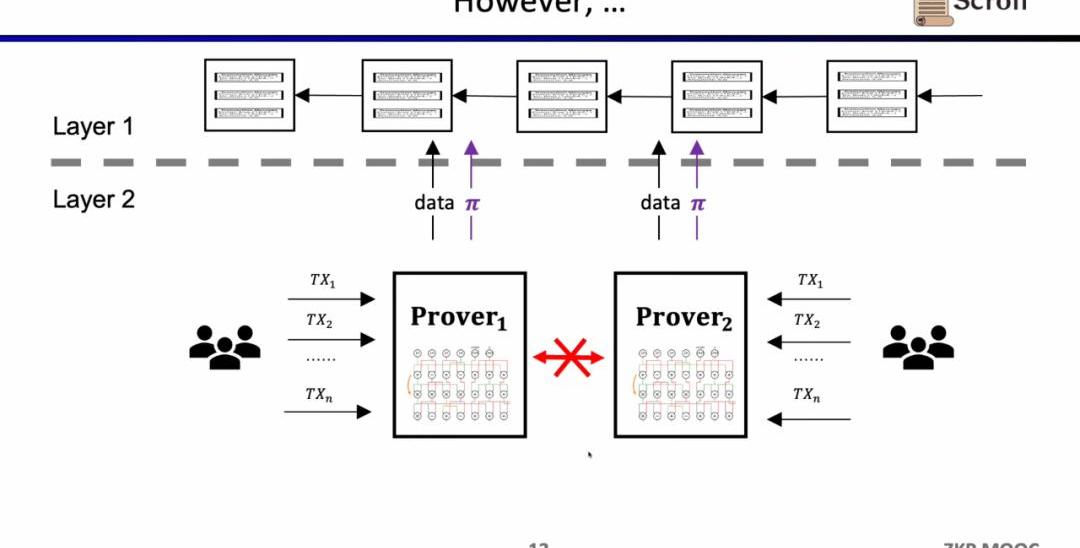
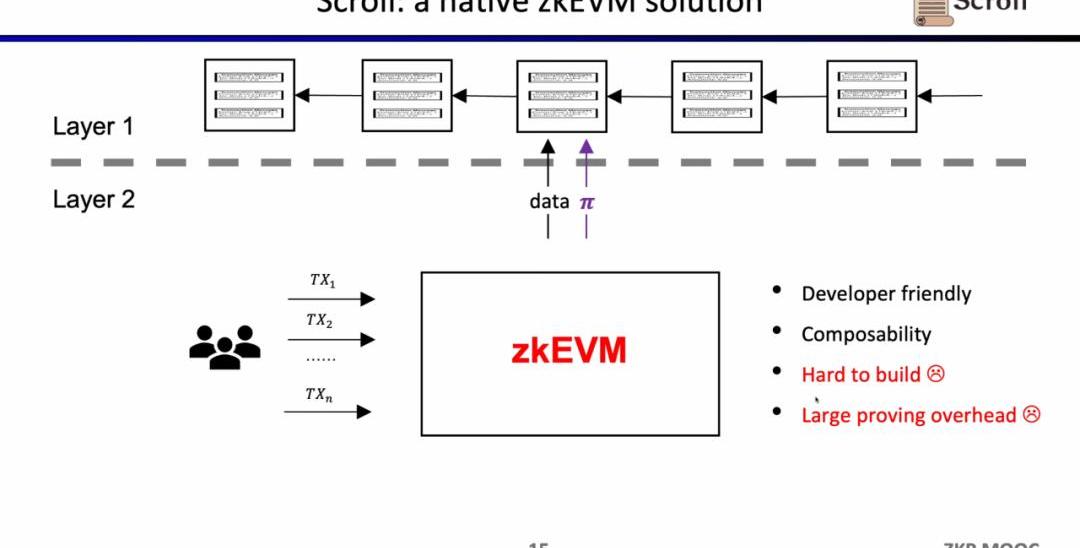
Scroll所要做的是原生的zkEVM方案，是一種通用型的ZK-Rollup。這樣不僅對用戶而言更友好，對于開發者而言也可以獲得在L1上的開發體驗。當然這背后的開發難度非常之大，并且現在的證明生成的代價也非常高。

Web3錢包開發公司Scrimmage完成60萬美元融資:11月1日消息，Web3錢包開發公司Scrimmage宣布完成60萬美元Pre-Seed輪融資，IA Ventures和Eberg Capital領投，Techstars參投。

據悉，Scrimmage應用程序允許用戶在購買NFT的同時獲得SCRIM獎勵。該公司聯合創始人Dan Taren和Matt Dever曾在美國銀行和花旗集團擔任金融分析師。（Sporttechie）[2022/11/1 12:03:39]

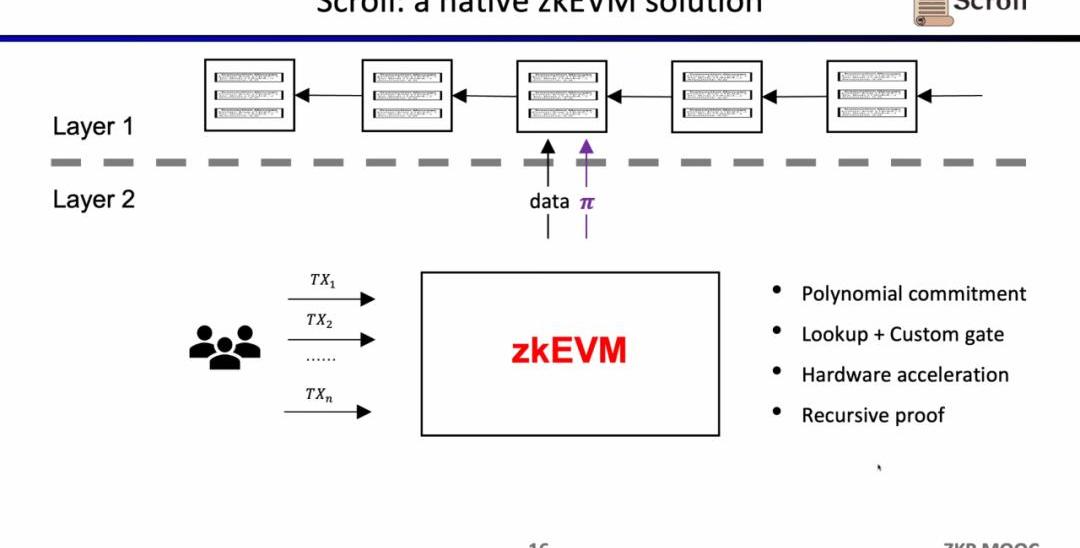
幸運的是，零知識證明的效率在過去兩年里已經大幅提高了，這也是為什么在最近兩年zkEVM變得如此受歡迎。至少有四個原因讓它變得可行，第一是多項式承諾的出現，在原先Groth16證明系統下，約束的規模非常之龐大，而多項式承諾可以支持更高階的約束，縮小證明規模；第二是查找表和自定義門的出現，可以支持更靈活的設計，使證明更加高效；第三是硬件加速方面的突破，通過GPU，FPGA和ASIC可以將證明時間縮短1-2個數量級，第四是在遞歸證明下，可以將多個證明壓縮成一個證明，使得證明變得更小更易于驗證。所以結合這四個因素，零知識證明的生成效率要比兩年前高出三個數量級，這也是Scoll的起源。

根據JustinDrake的定義，zkEVM可以分為三類，第一類是語言級別的兼容，主要原因是EVM不是為ZK而設計，有很多對ZK不友好的操作碼，因此會造成大量的額外開銷。因此像Starkware和zkSync選擇在語言層面將Solidity或者Yul編譯到ZK友好的編譯器中。

第二類是Scroll在做的字節碼層面的兼容，是直接證明EVM的字節碼處理正確與否，直接繼承了以太坊的執行環境。在這里可做的一些取舍是，使用和EVM不一樣的狀態根，例如使用ZK友好的數據結構。Hermez和Consensys也在做類似的事情。

第三類是共識層面的兼容，這里的取舍在于不僅需要保持EVM不變，還包括儲存結構等實現以太坊完全兼容，代價是需要更長的證明時間。而Scroll正在和以太坊基金會的PSE團隊合作構建，來實現以太坊的ZK化

從0到1構建zkEVM

第二部分，張燁向大家展示了如何從零開始建立ZKVM。

完整流程

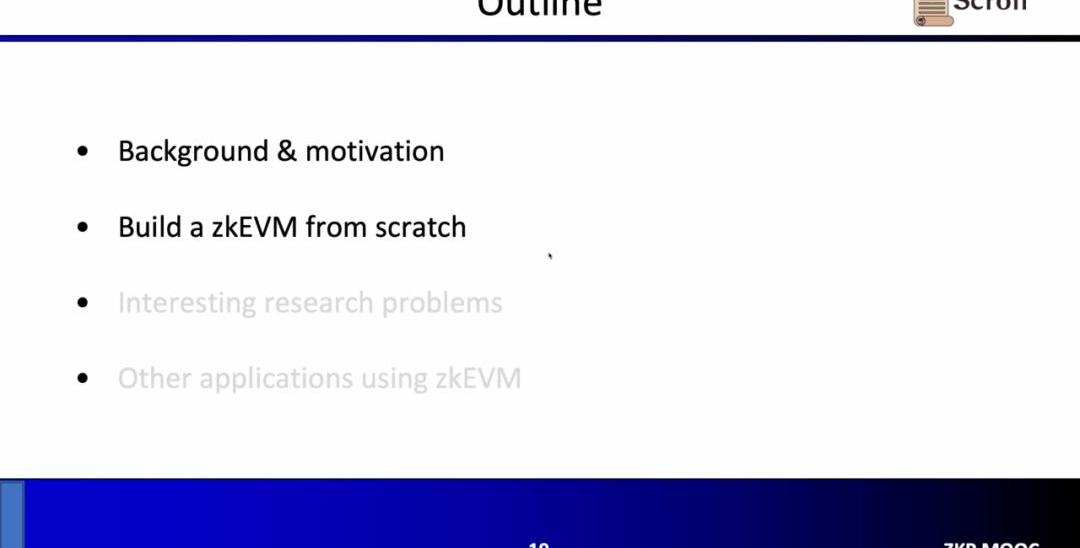
首先，在ZKP的前端部分，你需要通過數學的算術化來表示你的計算，最常用的就是線性的R1CS，以及Plonkish和AIR。通過算術化得到約束后，在ZKP的后端你需要運行證明算法，來證明計算正確性，這里列舉了最常用的多項式交互式諭示證明(PolynomialIOP)和多項式承諾方案(PCS)。

代幣標準化協議Smart Token Labs與Klaytn合作，計劃將TokenScript引入Klaytn網絡:3月28日消息，代幣標準化協議Smart Token Labs與韓國區塊鏈平臺Klaytn達成合作，Smart Token Labs計劃將TokenScript（一種智能代幣接口）引入Klaytn網絡，為其在Web3、游戲、NFT和元宇宙的發展計劃提供基礎設施服務。[2022/3/28 14:22:15]

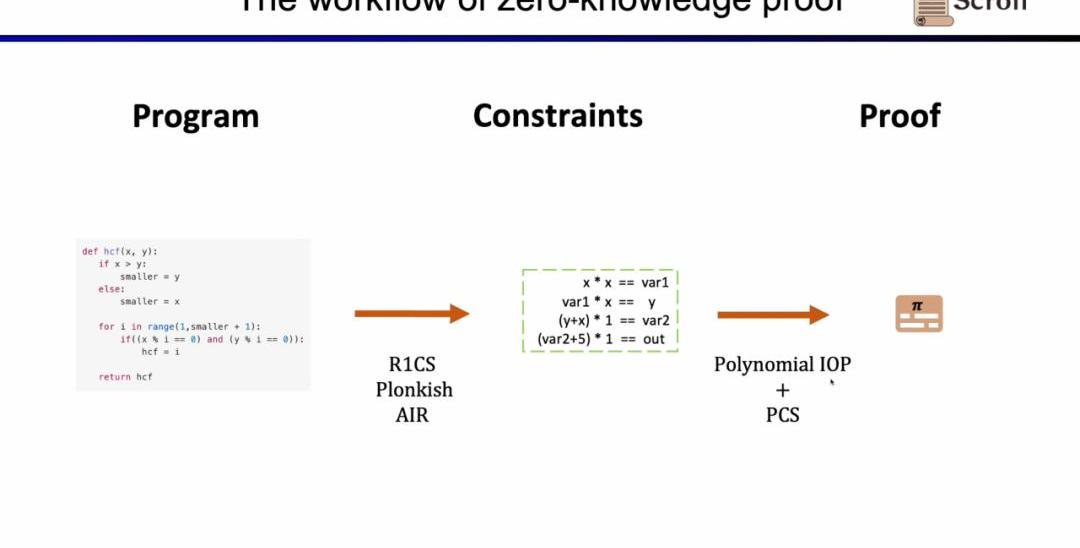
在這里我們需要證明zkEVM，Scroll使用的是Plonkish，PlonkIOP，以及KZG的組合。

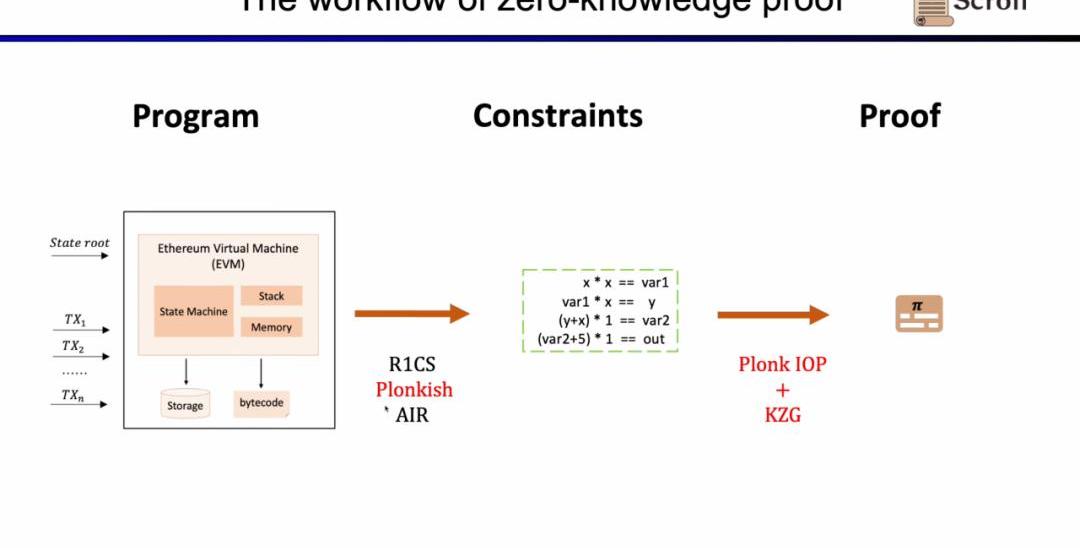
為了理解我們為什么使用這三者的方案。我們首先從最簡單的R1CS開始，R1CS中的約束，是線性組合乘以線性組合等于線性結合。你可以加上任何變量的線性組合而沒有額外的開銷，但是在每個約束中階數最大是2。因此對于階數較高的運算，需要的約束就越多。

而在Plonkish中，你需要將所有的變量填入表格，包括輸入，輸出以及中間變量的見證。在此之上，你可以定義不同的約束。在Plonkish中有三種類型的約束可以使用。

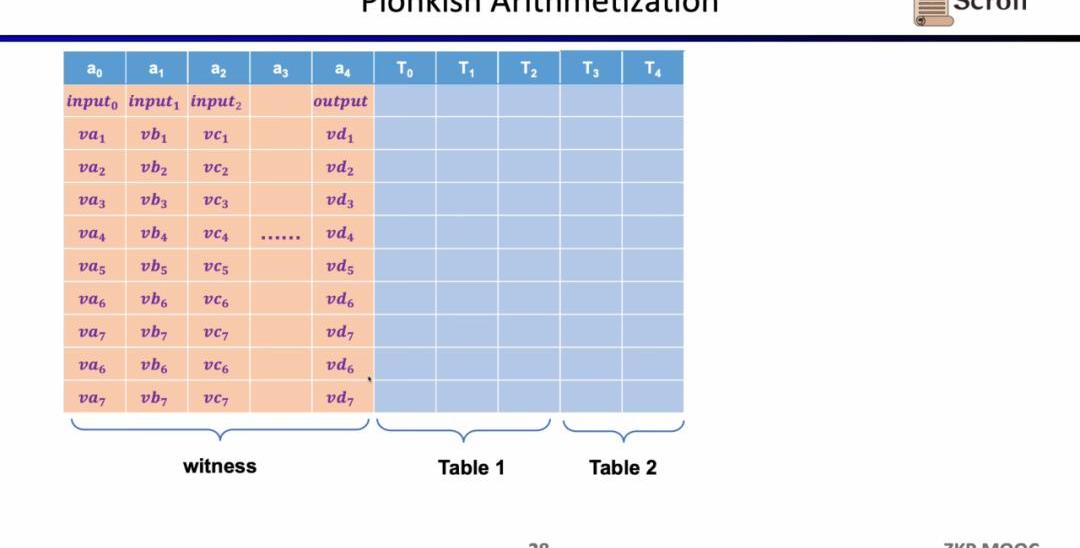
第一種約束是自定義門，你可以定義不同單元格之間的多項式約束關系，例如va3*vb3*vc3-vb4=0。相比R1CS來說，階數可以更高，因為你可以定義任何一個變量的約束，并且可以定義一些非常不一樣的約束。

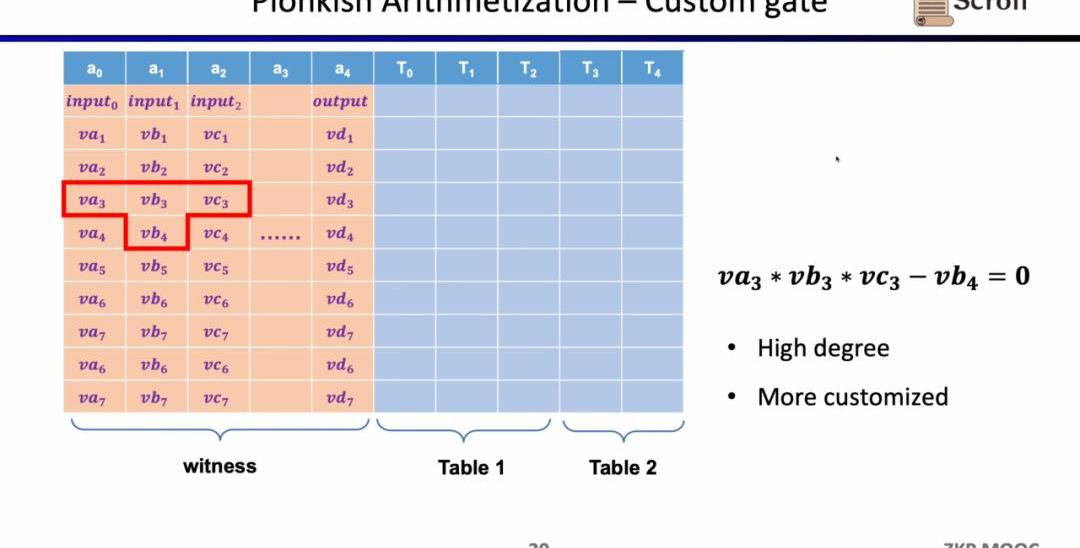
第二種約束是Permuation，即等價性校驗(equalitychecks)。可以用來檢查不同單元格的等價性，常用于關聯電路中的不同門，比如證明上一個門的輸出等于下一個門的輸入。

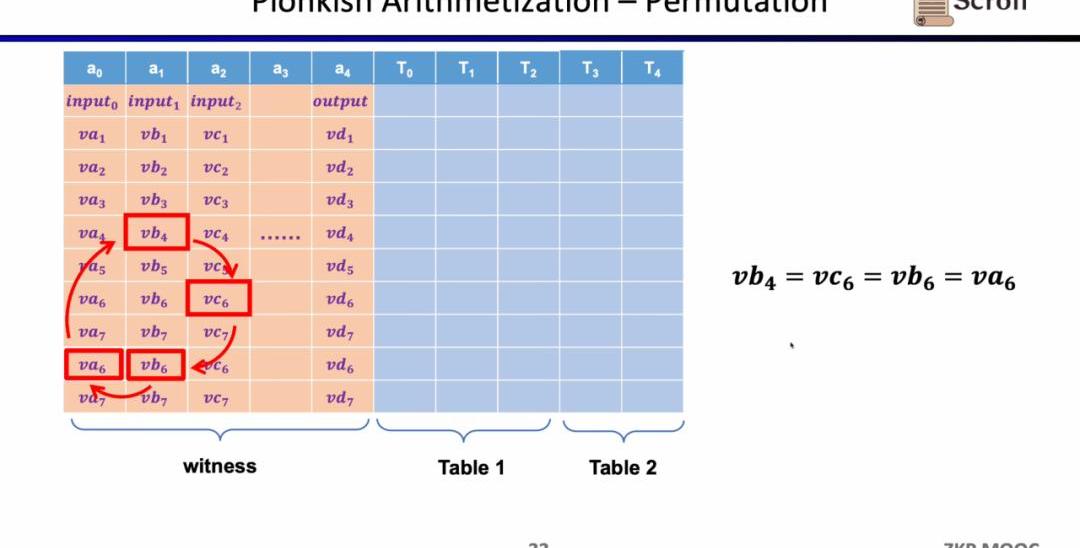
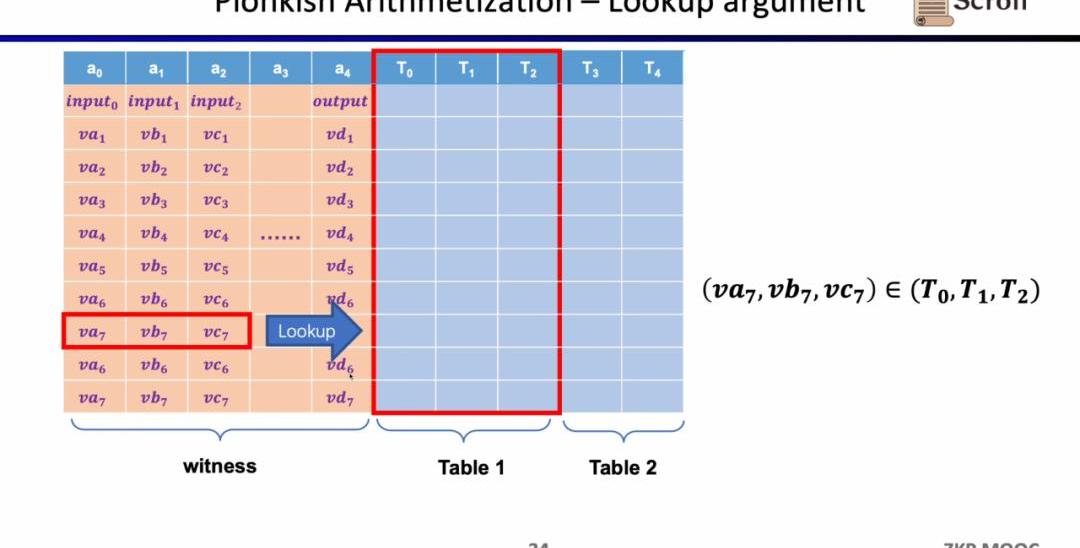
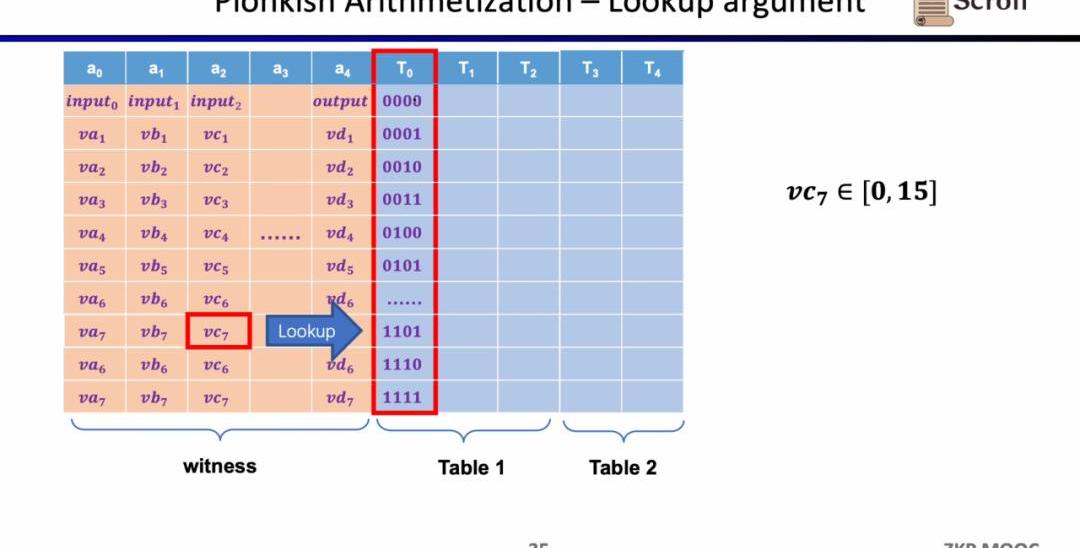
最后一種約束是查找表(LookupTable)。我們可以將查找表理解成變量之間存在一個關系，該關系可以表示成一個表。例如我們想要證明vc7在0-15范圍內，在R1CS中你首先需要把這個數值分解為4位二進制，然后證明每位在0-1的范圍內，這將需要四個約束。而在Plonkish中，你可以將所有可能的范圍列在同一列，只需要證明vc7屬于該列即可，這對范圍證明非常高效，在zkEVM中，查找表對于證明內存讀寫非常有用。

Optimistic推出JavaScript中的合約模擬Smock v2:官方消息，以太坊二層擴容方案Optimistic Ethereum推出JavaScript中的合約模擬Smock v2，無需在Solidity中編寫模擬合約。據Optimistic介紹，智能合約測試歷來很困難或困惑，必須在Solidity中編寫測試代碼；必須重新編譯測試合約才能改變測試；測試合約和目標合約共享相同的鏈狀態。而Smock v2具有以下功能：偽造任何合約；操作任何合約函數；對調用進行斷言；創建由真實合約支持的模擬；在模擬中操作變量等。[2021/8/12 1:50:38]

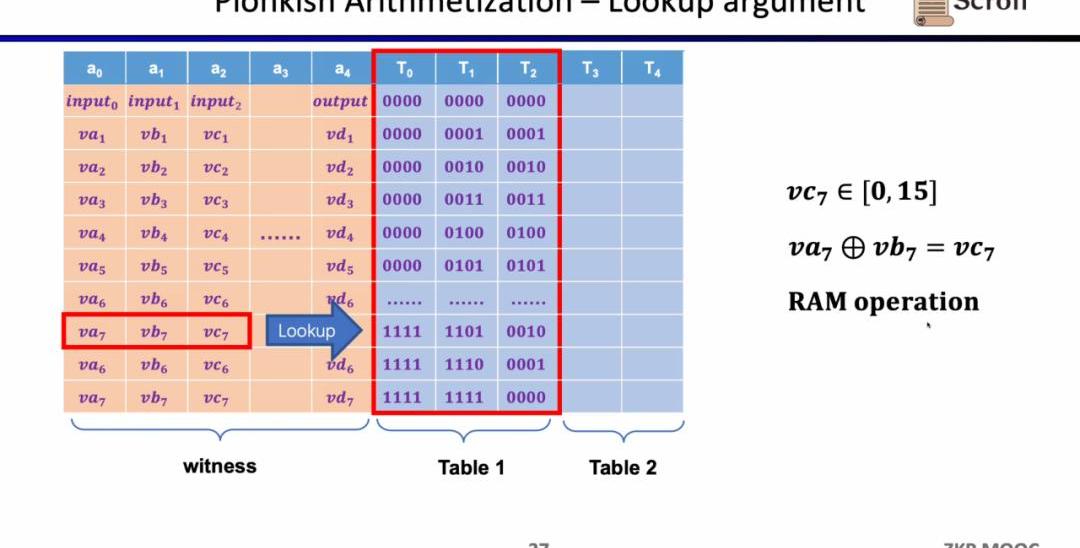
小結一下，Plonkish同時支持自定義門，等價性校驗和查找表，可以非常靈活的滿足不同的電路需要。簡單對比下STARK，STARK中每一行是一個約束，約束需要表示行與行之間的狀態轉換，但Plonkish中的自定義約束靈活性顯然更高。

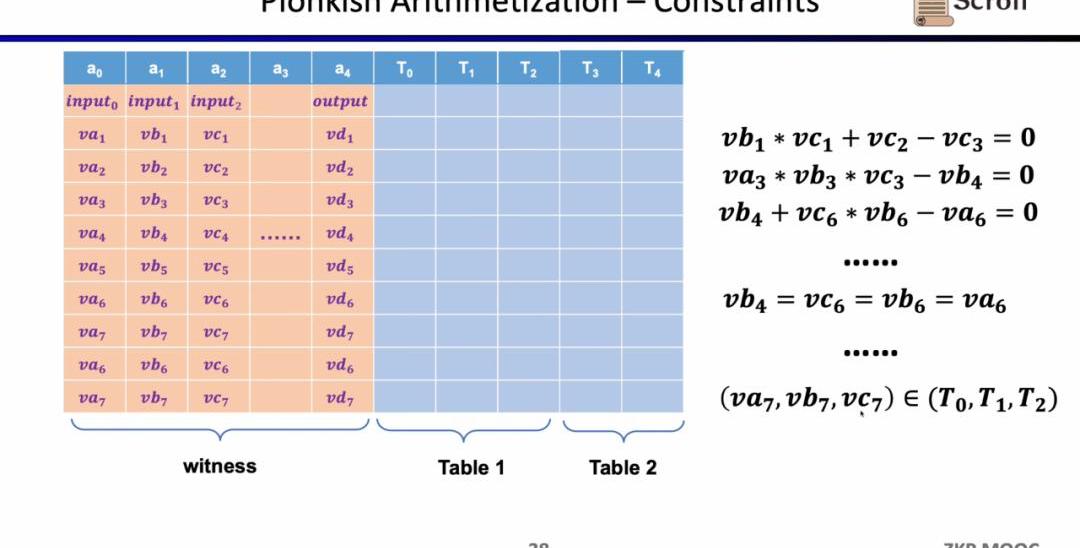
現在的問題是在zkEVM中，我們如何選擇前端。對于zkEVM主要有四個挑戰。第一個挑戰是EVM的字段是256位，這意味著需要高效得對變量進行范圍約束；第二個挑戰是EVM有很多ZK不友好的操作碼，因此需要非常大規模的約束來證明這些操作碼，例如Keccak-256；第三個挑戰是內存讀寫問題，你需要一些有效的映射來證明你所讀取的和之前所寫入的是一致的；第四個挑戰是EVM的執行蹤跡是動態變化的，因此我們需要自定義門來適配不同的執行蹤跡。出于上述的考慮，我們選擇了Plonkish。

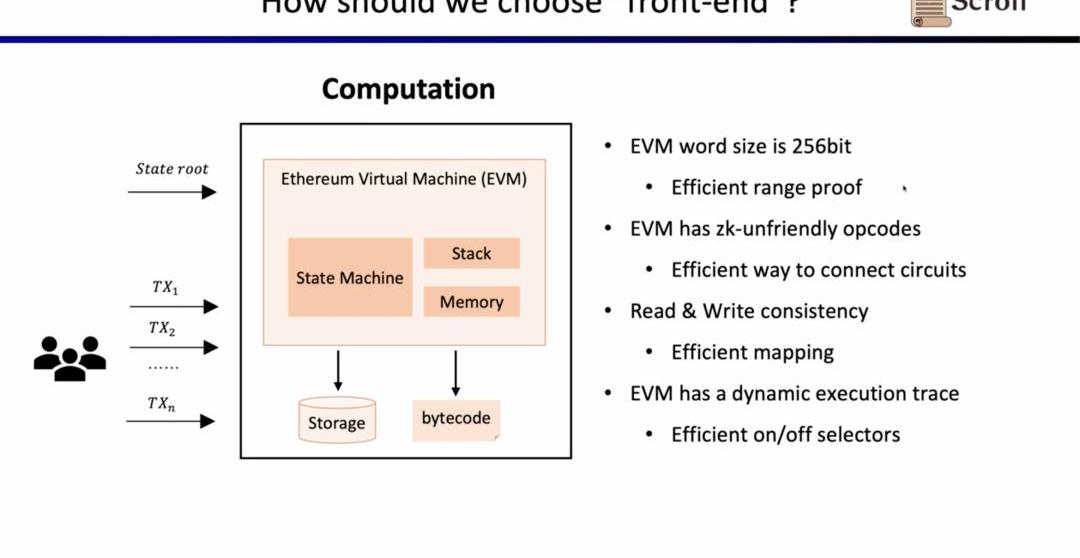
接下來，我們看zkEVM的完整流程，基于初始的全局狀態樹，一筆新的交易進來后，EVM會讀取存儲和調用的合約的字節碼，根據交易生成相應的執行蹤跡例如PUSH,PUSH,STORE,CALLVALUE，然后逐步執行更新全局狀態，得到交易后的全局狀態樹。而zkEVM是將初始的全局狀態樹，交易本身，以及交易后的全局狀態樹作為輸入，根據EVM的規范，來證明執行蹤跡的執行正確性。

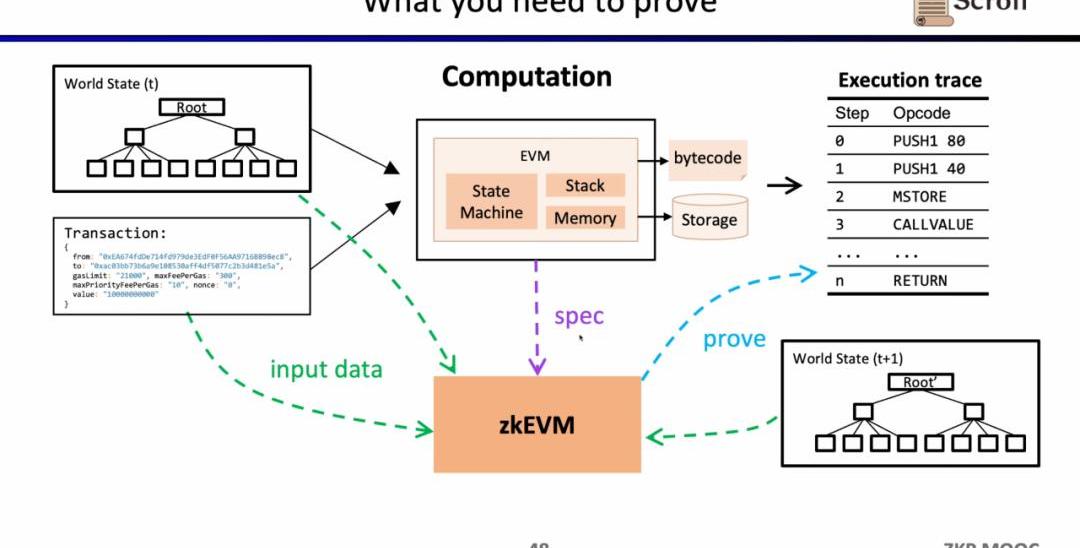
深入EVM電路細節，每一步執行蹤跡都有對應的電路約束。具體來說，每一步的電路約束包含StepContext，CaseSwitch，OpcodeSpecificWitness。StepContext包含執行蹤跡對應的codehash，剩余gas和計數器；CaseSwitch包含所有的操作碼，所有的錯誤情況，以及該步的相應操作；OpcodeSpecificWitness包含了操作碼所需的額外見證，例如運算數等。

TrustBase團隊完成subscript語言的Web3基金會Grant資助計劃項目交付:據官方消息，近日，波卡智能合約語言subscript的開發團隊成功向Web3基金會交付了subscript語言的核心庫功能。

subscript語言是由TrustBase維護的用于波卡wasm智能合約的語言框架，方便web開發者使用wasm智能合約構建DApp應用。開發團隊正在開發subscript合約語言的后續功能，完善波卡智能合約的應用生態。[2021/2/2 18:41:38]

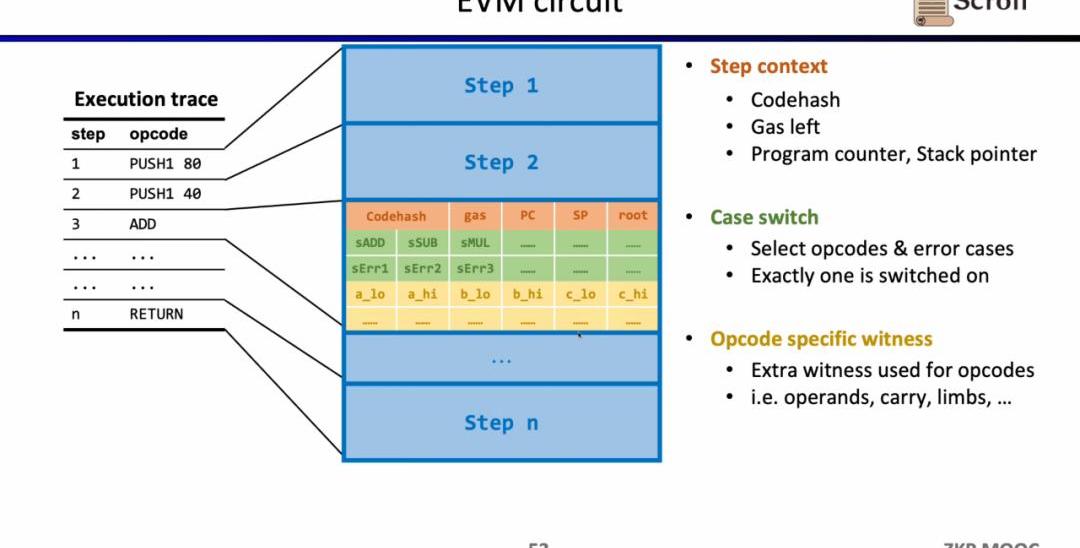
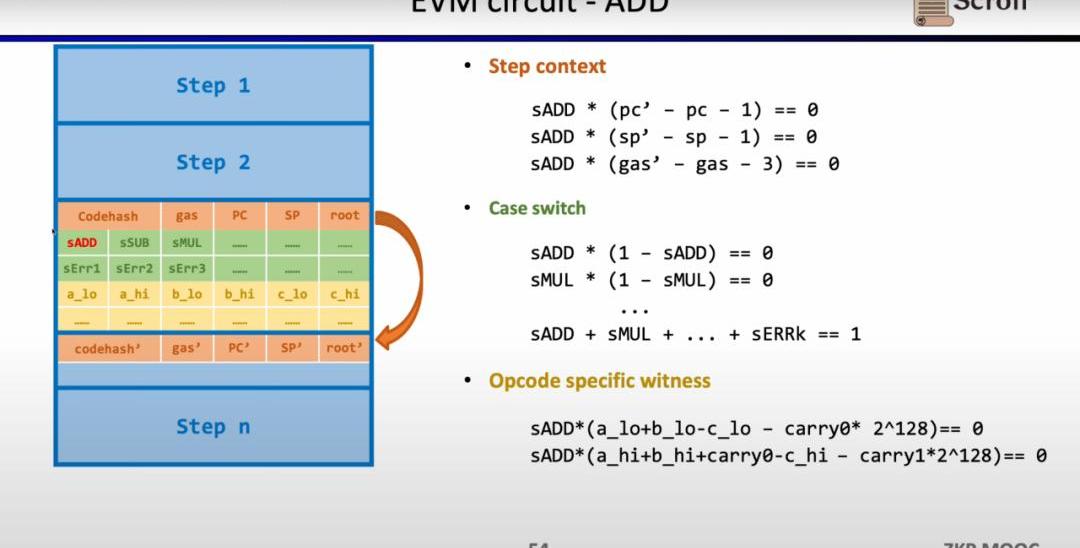
以簡單的加法為例，需要確保加法的操作碼的控制變量sADD設置為1，其他操作碼控制變量均為零。在StepContext中，通過設置gas'-gas-3=0來約束消耗的gas等于3，同理約束計數器，棧指針在該步后累加1；在CaseSwitch中，通過操作碼控制變量和為1來約束該步為加法操作；在OpcodeSpecificWitness中，對運算數的實際加法進行約束。

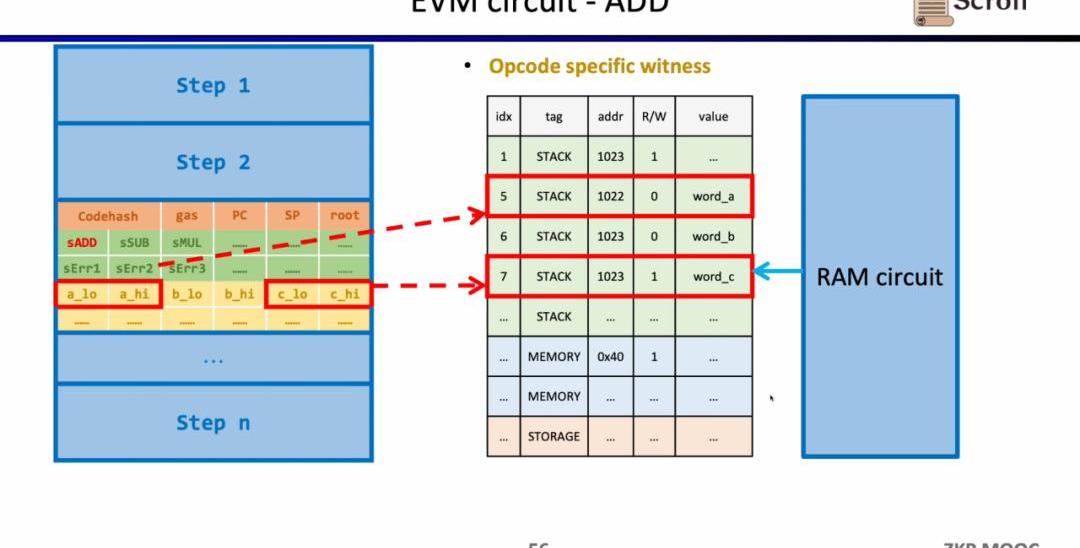
此外還需要額外的電路約束，來保證運算數從內存讀取的正確性。這里我們首先需要構建一個查找表來證明運算數屬于內存。并通過內存電路(RAMCircuit)來驗證內存表的正確性。

同樣的方法可以適用于zk不友好的哈希函數，構建哈希函數的查找表，將執行蹤跡中的哈希輸入和輸出映射到查找表，利用額外的哈希電路(HashCircuit)來驗證哈希查找表的正確性。

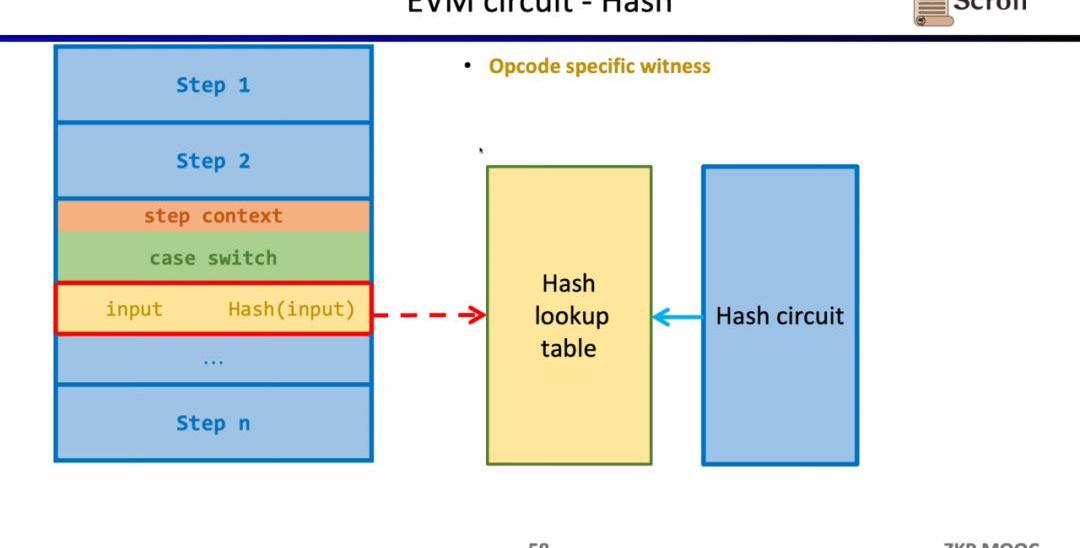
現在我們來看zkEVM的電路架構，核心的EVM電路用于約束執行蹤跡每一步的正確性，在一些EVM電路約束難度較大的地方，我們通過查找表來映射，包括FixedTable,KeccakTable,RAMTable,Bytecode,Transaction,BlockContext，然后利用單獨的電路來約束這些查找表，例如Keccak電路用于約束Keccak表。

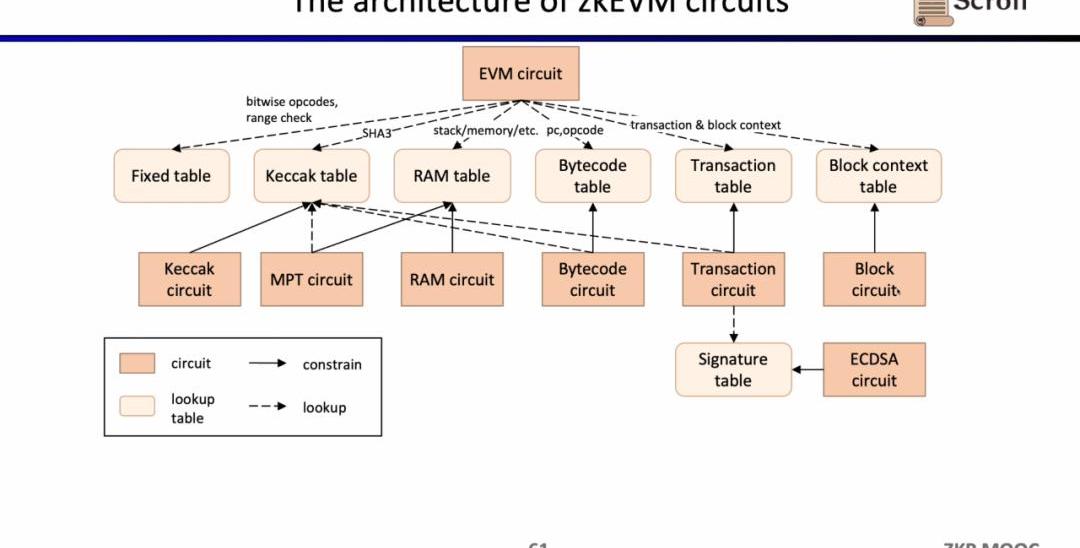
小結一下，zkEVM的完整工作流如下圖所示。

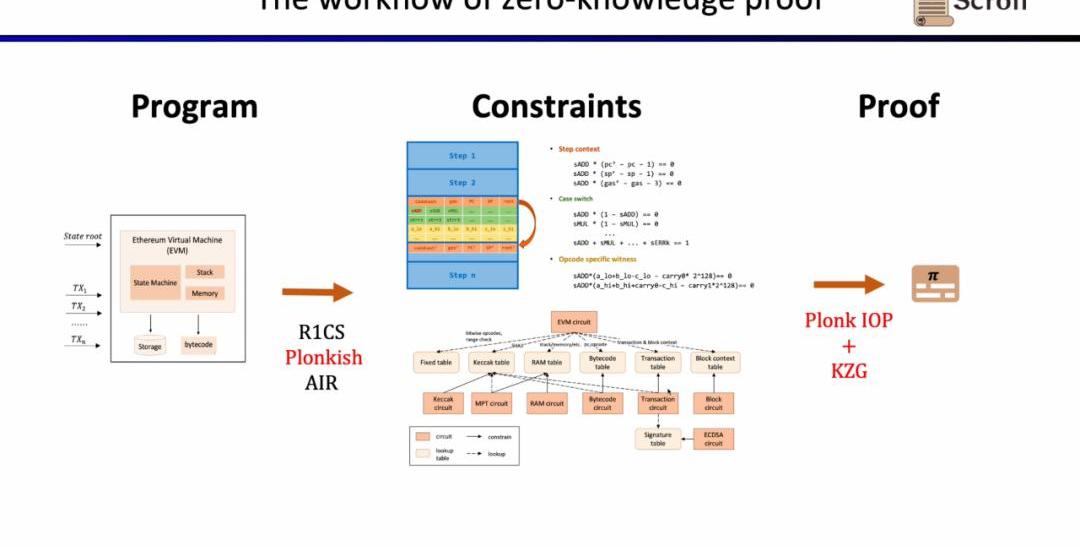
證明系統

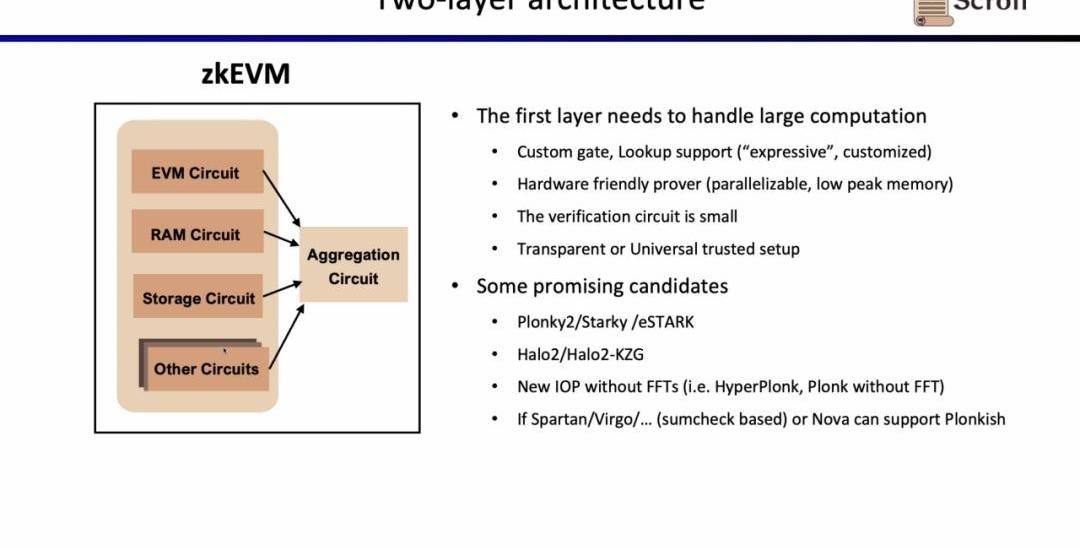
因為在L1上直接驗證上述的EVM電路，內存電路，存儲電路等，開銷巨大，Scroll的證明系統采用了兩層架構。

SCRY參加日本關于區塊鏈技術與應用的研討會:日前，SCRY團隊受日本合作伙伴邀請，前往東京Atogo green hills Mori tower，進行了關于區塊鏈技術與應用的研討會，SCRY介紹了項目立項的原因以及希望讓區塊鏈技術更好的服務全世界的美好愿景，對于SCRY特有的底層雙鏈結構以及其快速的傳輸速度和穩定性進行了詳細講解，同時將在7月份發布的第一個Dapp應用里融合了社交與數據預測等趣味玩法。[2018/4/2]

第一層負責直接證明EVM本身，需要大量的計算來生成證明。因此第一層證明系統要求支持自定義門和查找表，對硬件加速友好，在低峰值內存下并行生成計算，且驗證電路規模小，可以快速驗證。有前景的可選方案包括Plonky2，Starky，eSTARK，它們前端基本上都使用Plonk，但后端可能使用了FRI，并且都滿足上述的四個特性。另一類可選的方案包括Zcash所開發的Halo2，以及KZG版本的Halo2。

還有一些新的證明系統也有很有前景，例如最近移除了FFT的HyperPlonk，而NOVA證明系統可以做到更小的遞歸證明。但它們在研究中只支持R1CS，如果他們未來可以支持Plonkish并且應用于實踐，將非常實用高效。

第二層證明系統用于證明第一層證明的正確性，需要可以在EVM中高效進行驗證，理想情況下，最好也是硬件加速友好并且支持transparent或者universalsetup。有前景的可選方案包括Groth16和列數較少的Plonkish證明系統。Groth16仍然是目前研究中證明效率極高的代表，而Plonkish證明系統在列數較少的情況下，也可以達到較高的證明效率。

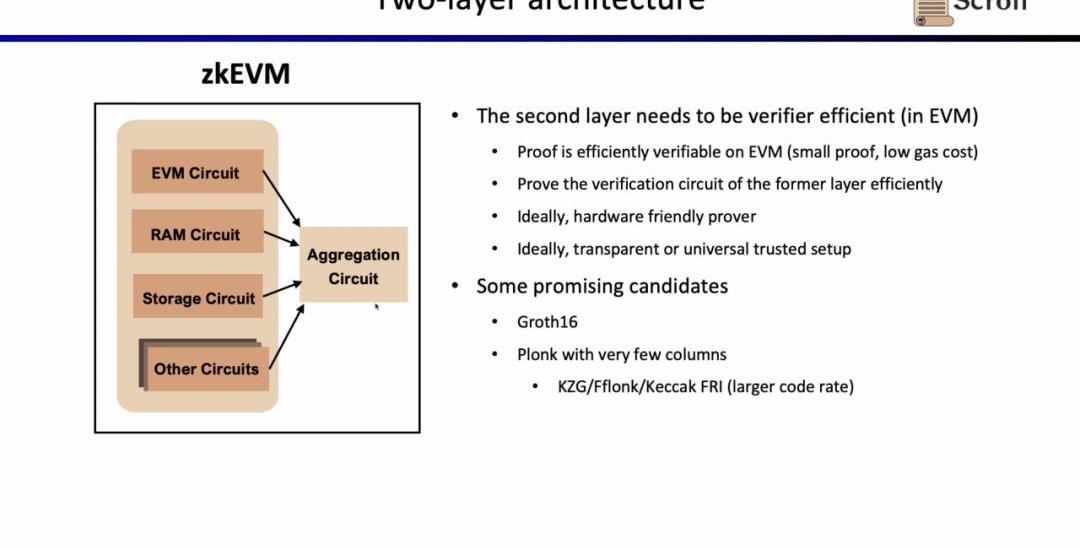
在Scroll，我們在兩層證明系統中我們都采用了Halo2-KZG證明系統。因為Halo2-KZG可以支持自定義門和查找表，在GPU硬件加速下性能良好，且驗證電路規模小，可以快速驗證。區別在于我們在第一層證明系統中我們使用了Poseidon哈希，進一步提高證明效率，而第二層證明系統因為直接在以太坊上驗證，仍然使用了Keccak哈希。Scroll也在探索多層證明系統的可能性，來進一步聚合第二層證明系統生成的聚合證明。

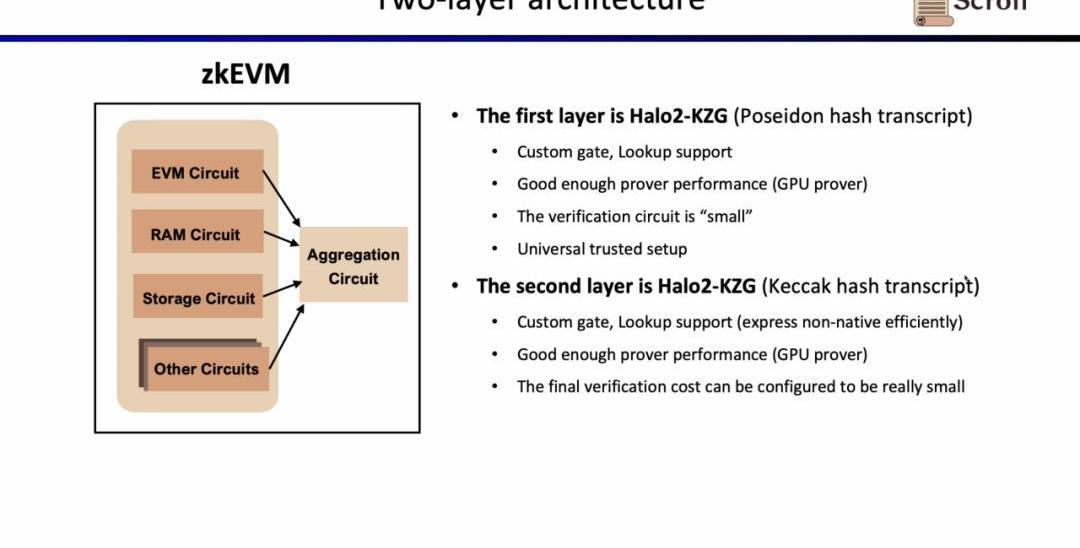
當前實現下，Scroll的第一層證明系統EVM電路有116列，2496個自定義門，50個查找表，最高階數為9，1MGas下需要2^18行；而第二層證明系統的聚合電路僅有23列，1個自定義門，7個查找表，最高階數為5，為了聚合EVM電路，內存電路，存儲電路，需要2^25行。

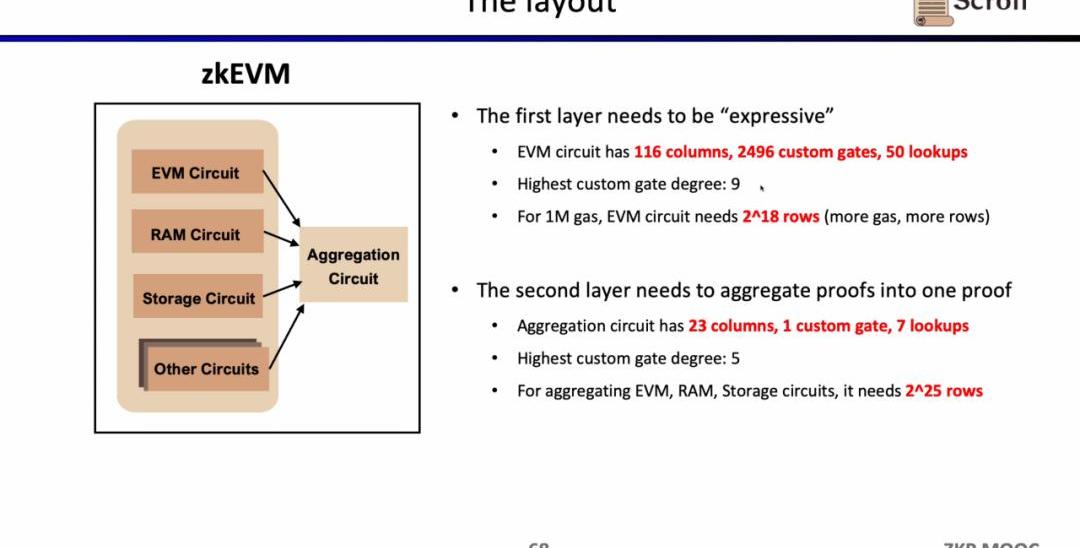
Scroll在GPU硬件加速方面也做了非常多的研究和優化工作，對于EVM電路，優化后的GPU證明者僅需30s，相較CPU證明者提升了9倍的效率；而對于聚合電路，優化后的GPU證明者僅需149s，相較CPU提升了15倍的效率。在當前的優化條件下，1MGas第一層證明系統大約需要2分鐘，第二層證明系統大約需要3分鐘。

有趣的研究問題

第三部分，張燁談論了一些Scroll在構建zkEVM過程中有趣的研究問題，從前端的算術化電路到證明者的實現。

電路

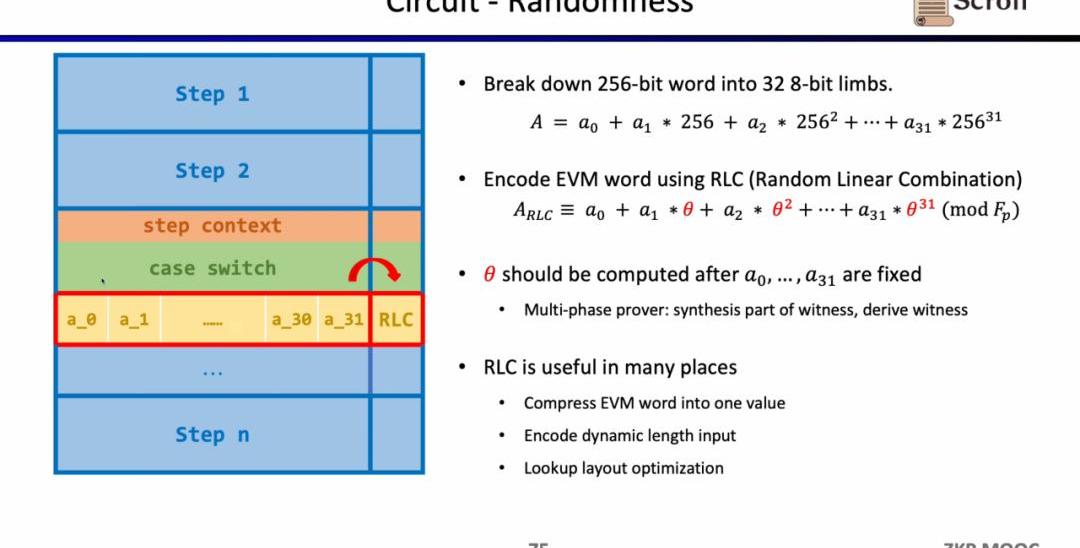
首先是電路中的隨機性，因為EVM字段是256位，我們需要將其拆分成32個8位的字段，從而更高效得進行范圍證明。隨后我們使用隨機線性組合(RandomLinearCombination,RLC)的方法，利用隨機數將32個字段編碼成1個，只需要驗證該字段就可以驗證原始的256位字段。但是問題在于隨機數的生成需要在拆分字段之后，才能確保不被篡改。

因此Scroll和PSE團隊提出了多階段證明者的方案，來確保在字段拆分之后，再利用隨機數生成RLC，該方案被封裝在了ChallengeAPI中。RLC在zkEVM中有許多應用場景，不僅可以壓縮EVM字段成一個字段，也可以加密不定長的輸入，或是優化查找表的布局，但仍然有許多開放性的問題需要解決。

電路方面第二個有趣的研究問題是電路布局。Scroll前端之所以采用Plonkish，是因為EVM的執行蹤跡是動態變化的，需要能支持不同的約束，變化的等價性檢驗，而R1CS的標準化門需要更大的電路規模來實現。

但Scroll目前使用了2000多個自定義門來滿足動態變化的執行蹤跡，也在探索如何進一步優化電路布局，包括將Opcode拆分成MicroOpcode，或是復用相同表格內的單元格。

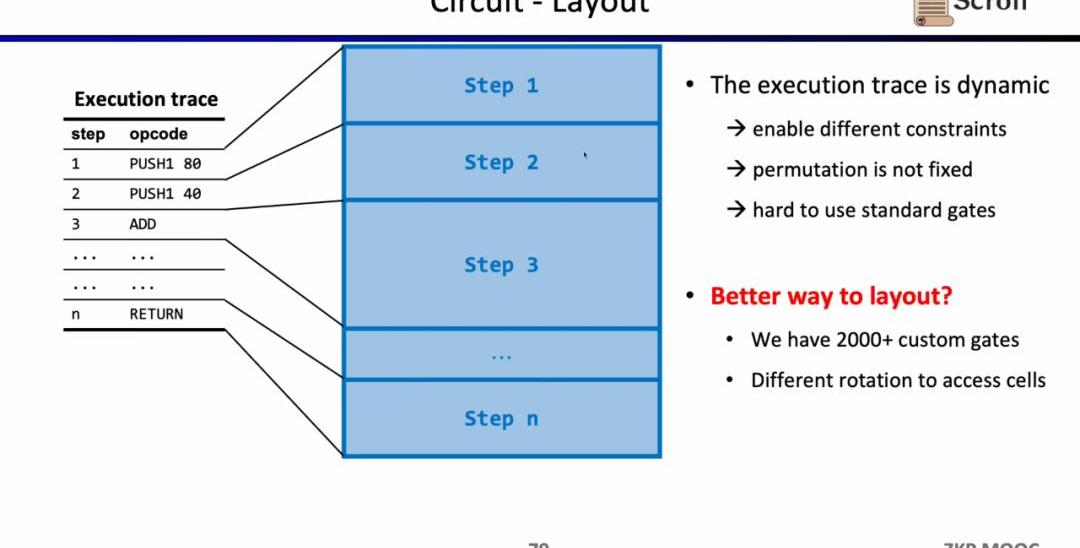
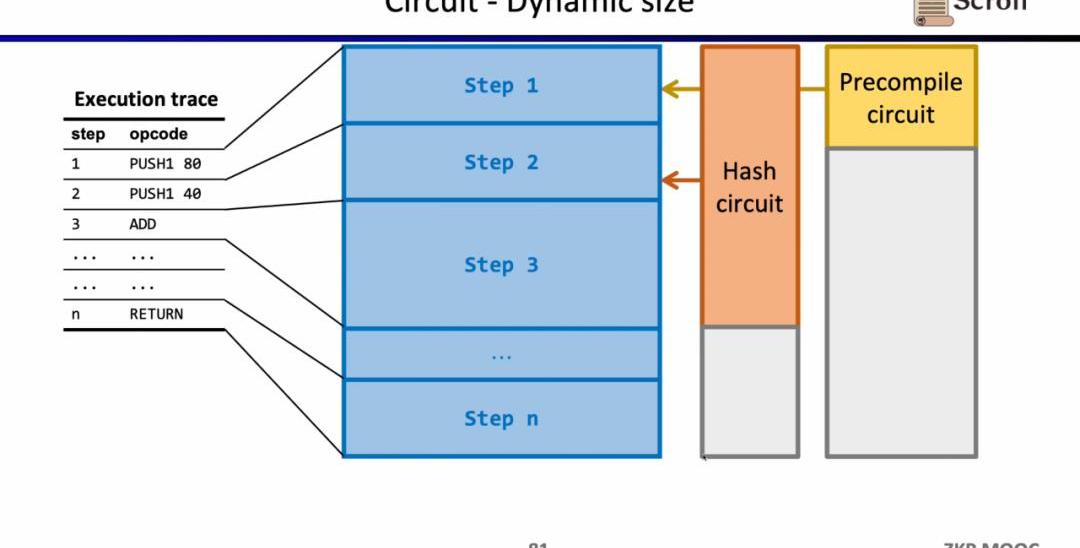
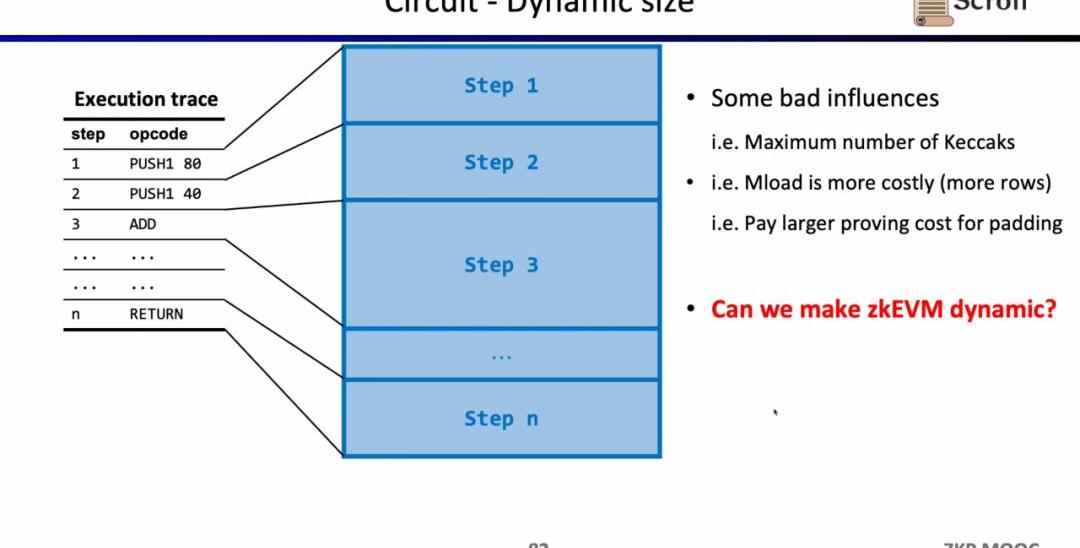
電路方面第三個有趣的研究問題是動態規模。因為不同的操作碼的電路規模不同，但為了滿足動態變化的執行蹤跡，每一步的操作碼都需要滿足最大的電路規模，例如Keccak哈希，因此我們實際上付出了額外的開銷。假設我們可以使zkEVM動態適應動態變化的執行蹤跡，這將節省不必要的開銷。

證明者

在證明者方面，Scroll在GPU加速上已經對MSM和NTT進行了大量的優化，但現在的瓶頸轉移到了見證生成和復制數據這塊。因為假設MSM和NTT占據了80%的證明時間，即使硬件加速可以將這部分效率提升若干個數量級，但原先見證生成和復制數據20%的證明時間將變成新的瓶頸所在。證明者的另一個問題是需要大量的內存，因此也需要探索更便宜更去中心化的硬件方案。

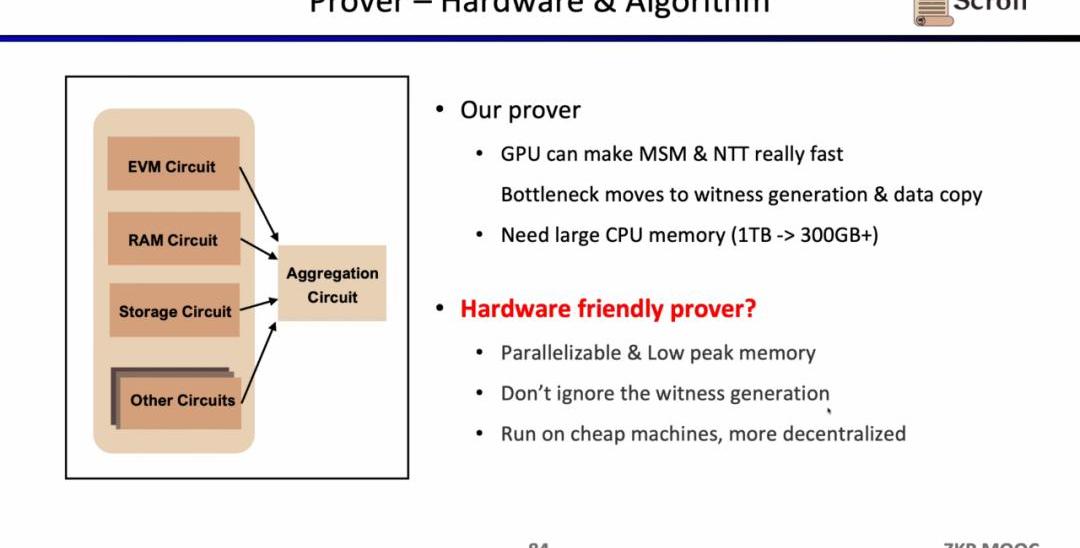
同時Scroll也在探索硬件加速和證明算法方面，來提升證明者的效率。目前主要有兩個大方向，或是切換至更小的域，例如使用64位的Goldilocks域，32位的梅森數等，或是堅持基于橢圓曲線的新證明系統，例如SuperNova。當然也有其他的一些別的可能路徑，歡迎有想法的朋友直接聯系Scroll。

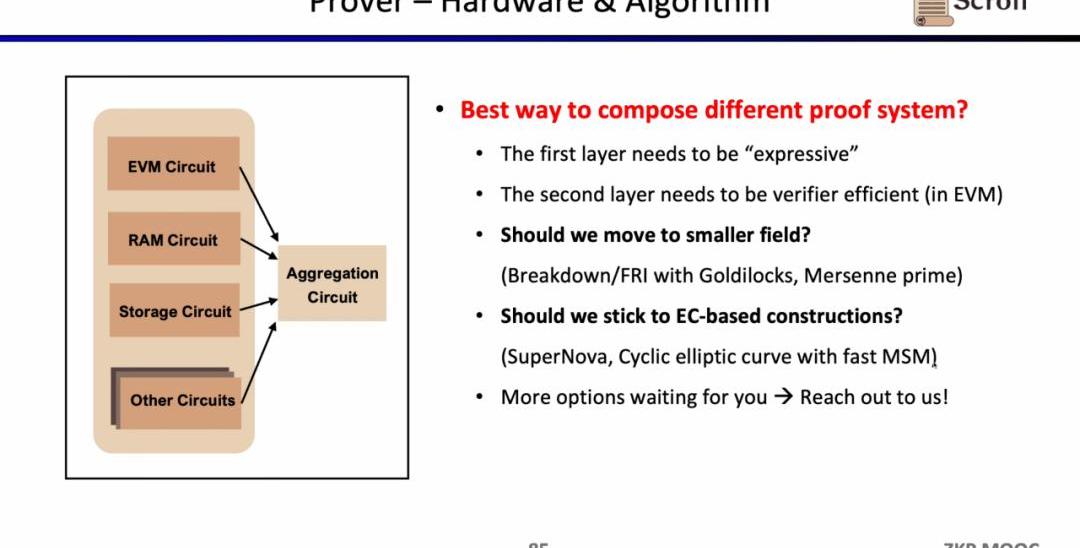
安全性

在構建zkEVM時，安全性是至關重要的。PSE和Scroll共同構建的zkEVM有大約3萬4千行代碼，從軟件工程角度，這些復雜的代碼庫在很長一段時間內是不可能沒有漏洞的。Scroll目前在通過大量的審計，包括業內最頂尖的審計公司，來審核zkEVM的代碼庫。

其他使用zkEVM的應用

第四部分探討了其他一些使用了zkEVM的應用。

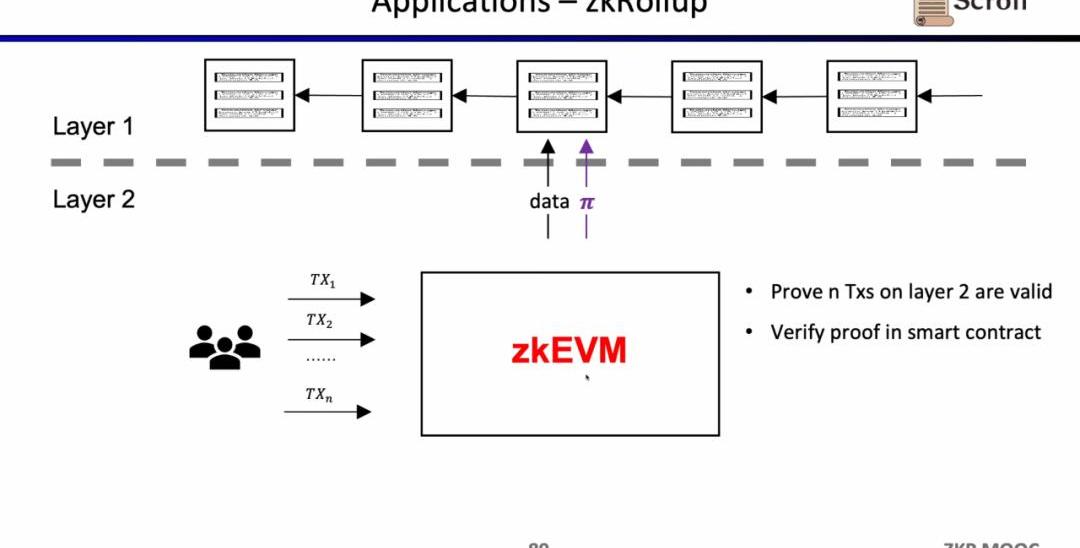
在zkRollup的架構中，我們通過在L1的智能合約，來驗證在L2上的n筆交易是有效的。

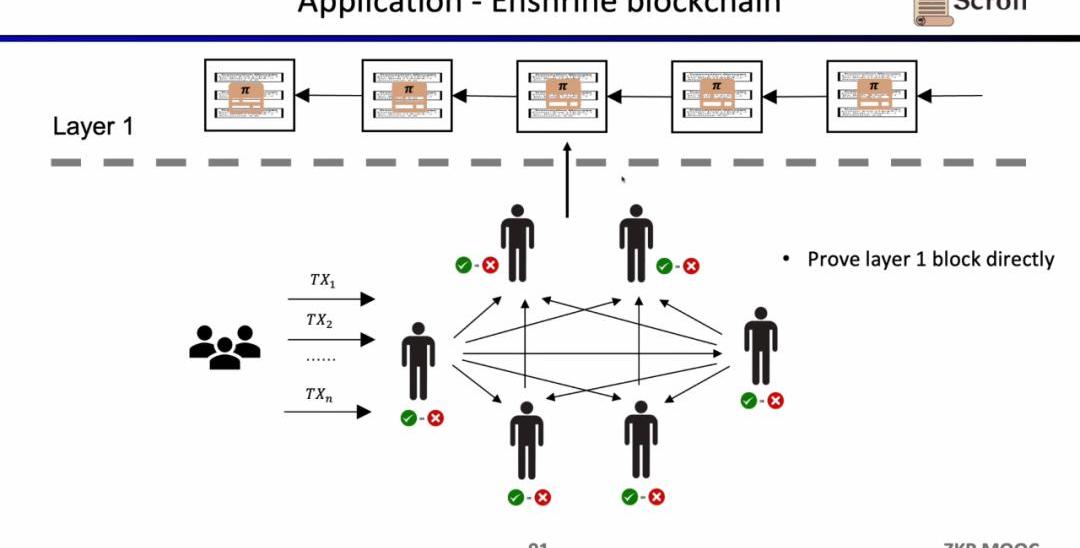
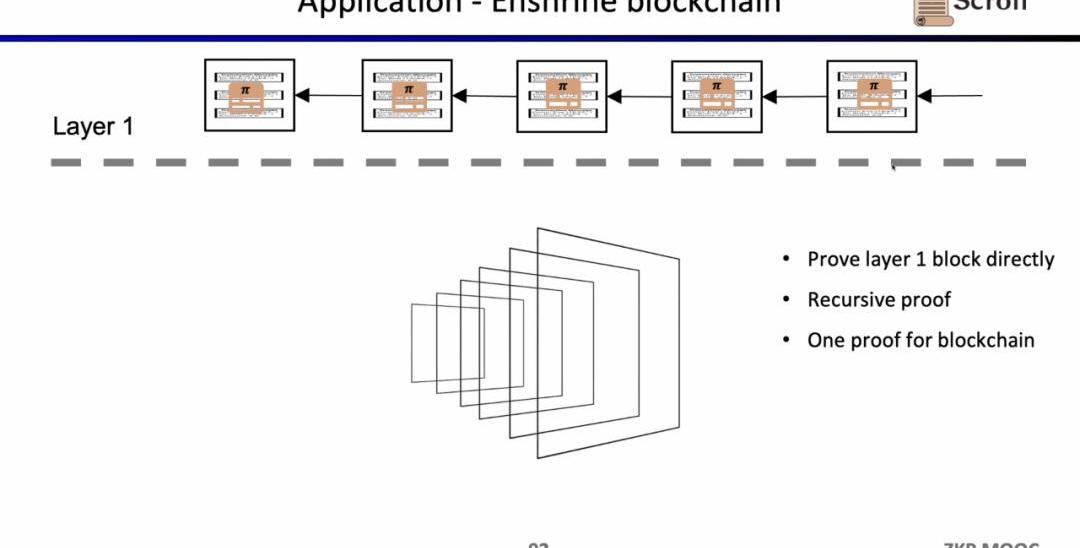
如果我們直接驗證L1的區塊，那么L1的節點就不需要重復執行交易，只需要驗證每一個區塊證明的有效性。這樣的架構方案稱為EnshrineBlockchain。目前在以太坊上直接實現難度非常之大，因為需要驗證整個以太坊區塊，其中會包括驗證大量簽名，隨之帶來更長的證明時間和更低的安全性。當然也已經有一些其他公鏈在通過遞歸證明，使用單個證明，來驗證整個區塊鏈，例如Mina。

因為zkEVM可以證明狀態轉換，它也可以被白帽所利用，來證明自己知道某些智能合約的漏洞，尋求項目方的賞金。

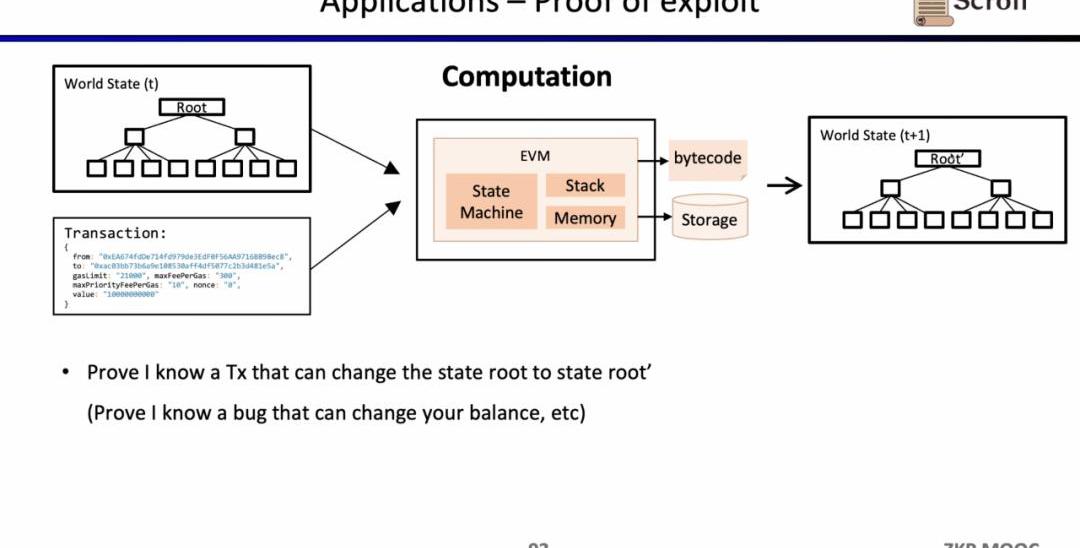
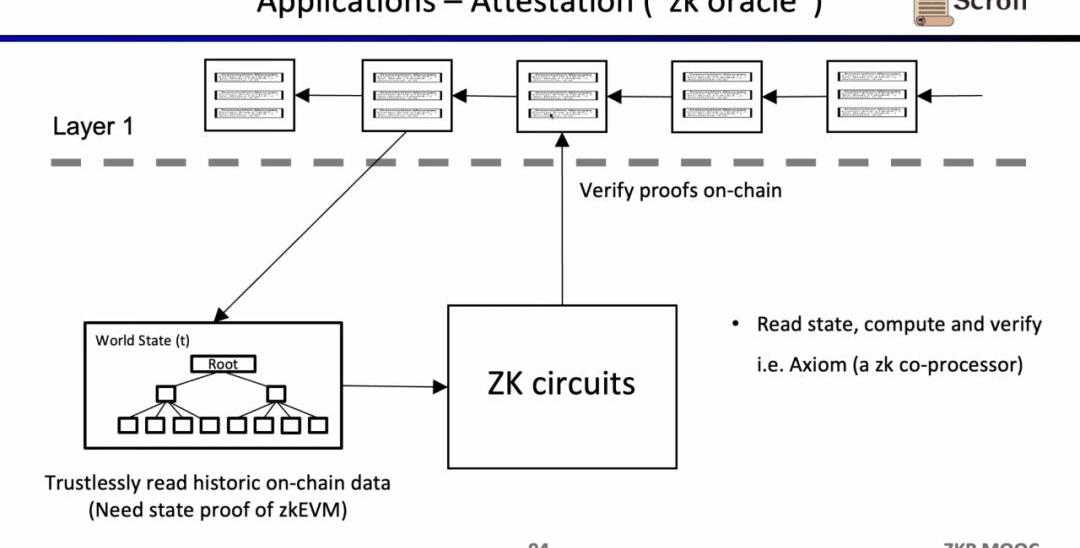
最后一個用例是，是通過零知識證明來證明對歷史數據的聲明，作為預言機來使用，目前Axiom正在做這方面的產品。最近的ETHBeijing黑客松上，GasLockR團隊正是利用了這一特性，證明了歷史的Gas開銷。

最后，Scroll正在構建zkRollup的以太坊通用擴容解決方案，使用了非常先進的算術化電路和證明系統，并且通過硬件加速構建快速的驗證器，證明遞歸。目前Alpha測試網已經上線，并穩定運行了很長時間。

當然仍然有一些有趣的問題需要解決，包括協議設計和機制設計，零知識工程和實際效率，歡迎大家加入Scroll一起構建！

Scroll

Website:?https://scroll.io/

Twitter:?https://twitter.com/Scroll_ZKP

Discord:?https://discord.com/invite/scroll

Github:?https://github.com/scroll-tech

Youtube:?https://www.youtube.com/@Scroll_ZKP

Tags：SCRROLLROLCROscrt幣總共多少枚roll幣怎么用BankRollEscrowed Illuvium

比特幣價格實時行情