VIT:Vitalik：如何權衡協議設計中的「封裝復雜性」和「系統復雜性」？_Gravity

以太坊協議設計的主要目標之一是最小化復雜性：使協議盡可能簡單，同時仍然使區塊鏈能夠做好一個有效的區塊鏈網絡需要做到的事情。以太坊協議在這方面還遠遠不夠完美，特別是因為它的很多部分都是在2014-16年設計的，當時我們對它的理解要少得多，但我們仍然在盡可能地積極努力降低復雜性。然而，這個目標的挑戰之一是復雜性很難定義，且有時，你必須在兩個引入不同種類復雜性和具有不同代價的選擇之間進行權衡。我們如何比較？有一個強大的智能工具可以讓我們對復雜性進行更細致的思考，那就是區分我們所謂的封裝復雜性(encapsulatedcomplexity)和系統復雜性(systemiccomplexity)。

Web3加速器GRAVITON公布首批入圍隊列，每個項目將獲5萬美元投資:5月9日消息，專注于新興市場的Web3加速器GRAVITON 已公布首批入圍隊列，覆蓋DeFi 支付、去中心化身份、現實世界資產標記化、NFT交易、GameFi等領域，其中包括Spydra、Strive、Zoth、Wall、GETSecured、Fetcch等七個印度項目。每個入圍項目將從Graviton獲得高達50,000美元的初始投資和來自全球Web3品牌的技術資助，以及與全球風險投資公司建立聯系并獲得未來機構資金的機會。[2023/5/9 14:52:57]

當一個系統的子系統內部復雜，但向外部呈現一個簡單的“接口”(interface)時，就是出現了「封裝復雜性」。當系統的不同部分甚至不能被清晰地分開，并且相互之間有復雜的交互時，「系統復雜性」就出現了。以下是幾個例子。BLS簽名vs.Schnorr簽名

BLS簽名和Schnorr簽名是兩種常用的可由橢圓曲線構成的加密簽名方案。BLS簽名在數學上看起來非常簡單：

Vitalik Buterin：FTX的欺詐行為比Mt.Gox和Luna更嚴重:11月12日消息，以太坊創始人Vitalik Buterin第一次對FTX崩盤事件發表直接評論，稱FTX的欺詐行為比Mt.Gox和Luna更嚴重，Mt.Gox看起來很粗狂，但從未過份粉飾自己，Luna也是如此，FTX則相反，它完全是在做合規的美德信號（與合規不一樣），第二種欺詐行為比第一種更嚴重。[2022/11/12 12:54:27]

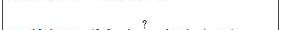
H是一個哈希函數，m是消息，k和K是私鑰和公鑰。到目前為止，很簡單。然而，真正的復雜性隱藏在e函數的定義中：橢圓曲線配對(ellipticcurvepairings)，這是所有密碼學中最難以理解的數學部分之一。現在，我們來看看Schnorr簽名。Schnorr簽名只依賴于基本的橢圓曲線。但是簽名和驗證邏輯有點復雜：

澳大利亞墨爾本出現有關Vitalik的街頭畫作:據Redidit網友爆料，近日，一幅畫有以太坊創始人Vitalik的街頭藝術創作出現在了澳大利亞墨爾本街頭。[2021/4/6 19:49:53]

所以…哪種類型的簽名“更簡單”？這取決于你在乎什么！BLS簽名具有巨大的技術復雜性，但復雜性都隱藏在e函數的定義中。如果你把e函數看作一個黑盒，BLS簽名實際上是非常簡單的。另一方面，Schnorr簽名的總體復雜性較低，但有更多的部分，能以一種微妙的方式與外部世界互動。例如：進行BLS多簽(兩個密鑰k1和k2的組合簽名)很簡單：只需σ1+σ2。但是Schnorr多簽名需要兩輪交互，并且需要處理一些棘手的KeyCancellation攻擊。Schnorr簽名需要生成隨機數，BLS簽名不需要。橢圓曲線配對通常是一個強大的“復雜性海綿”，因為它們包含大量封裝復雜性，但使解決方案具有更少的系統復雜性。這也適用于多項式承諾領域：將KZG承諾(需要配對)的簡單性與更復雜的內積證明(innerproductarguments，不需要配對)的內部邏輯進行比較。密碼學vs.加密經濟學

GTX（GravitationX）即將上線TokenBetter:據TokenBetter官方公告，GTX（GravitationX）將于2020年5月3日15:00上線TokenBetter。

GTX（GravitationX）的目標是通過結合 CryptoNote 協議和智能合約等一些經過驗證的最佳技術，創建一種獨特的先進區塊鏈技術，增強可靠性，隱私性，安全性，可用性和可移植性，從而實現創建私人智能合約。GTX（GravitationX）發行總量限定1億，永不增發。GTX擁有首個POD毀滅證明機制，百分之九十六的GTX將被摧毀，最后只剩下 4,000,000枚GTX。[2020/5/2]

在許多區塊鏈設計中出現的一個重要設計選擇是密碼學(cryptography)與加密經濟學(cryptoeconomics)的比較。這(比如在Rollups中)常常是在有效性證明(即ZK-SNARKs)和欺詐證明之間做出選擇。ZK-SNARKs是復雜的技術。雖然ZK-SNARKs工作原理背后的基本思路可以在一篇文章中解釋清楚，但實際上實現一個ZK-SNARK來驗證一些計算涉及到比計算本身多很多倍的復雜性(因此，這就是為什么用于EVM的ZK-SNARKs證明仍在開發中，而用于EVM的欺詐證明已經在測試階段)。有效地實現一個ZK-SNARK證明涉及到了對特殊目的進行優化的電路設計、使用不熟悉的編程語言以及許多其他挑戰。另一方面，欺詐證明本身就很簡單：如果有人提出挑戰，你只需直接在鏈上運行計算。為了提高效率，有時會添加一個二進制搜索方案，但即使這樣也不會增加太多的復雜性。雖然ZK-SNARKs很復雜，但它們的復雜性是封裝復雜性。另一方面，欺詐證明的相對較低的復雜性，是系統復雜性。以下是欺詐證明引入的一些系統復雜性的例子：它們需要謹慎的激勵工程來避免驗證者的困境。如果在達成共識的情況下完成，它們需要為欺詐證明提供額外的交易類型，同時還要考慮到如果許多參與者同時競相提交欺詐證明會發生什么。它們依賴于一個同步網絡。它們允許審查攻擊(censorshipattacks)也被用來進行盜竊。基于欺詐證明的Rollups要求流動性提供者支持即時提款。由于這些原因，即使從復雜性的角度來看，基于ZK-SNARKs的純加密解決方案也可能是長期安全的：ZK-SNARKs有著更復雜的部分，這是一些人在選擇ZK-SNARKs時必須考慮到的；但ZK-SNARKs有著更少的懸空警告，這是每個人都必須考慮到的。各種例子

聲音 | 江卓爾：分片提升容量難度大時間長 故而Vitalik提出使用BCH或者ETC作為以太坊數據層:7月25日消息，萊比特礦池CEO江卓爾表示，分布式系統（去中心化系統）有一個不可能三角，稱為分布式系統CAP定理，指的是在一個分布式系統中，Consistency（一致性）、 Availability（可用性）、Partition tolerance（分區容錯性），三者不可兼得。Vitalik提出用分片方法提升容量，但分片方法的難點是一致性，也就是CAP中的C，Consistency（一致性），這個是一個要挑戰不可能三角的開發，所以開發難度很大，時間長，所以Vitalik才提出使用BCH或者ETC作為以太坊數據層的短期方案，來解決ETH的燃眉之急。[2019/7/25]

PoW(中本聰共識)：較低的封裝復雜性，因為該機制非常簡單和容易理解，但有著更高的系統復雜性(如自私挖礦攻擊)。哈希函數：較高的封裝復雜性，但有著非常容易理解的屬性，因此系統復雜性很低。隨機洗牌算法：洗牌算法既可以是內部復雜(比如Whisk)，但卻能夠確保強大的隨機性，且易于理解；也可以是內部簡單，但卻能夠產生較弱且難以分析的隨機性屬性(比如系統復雜性)。礦工提取價值(MEV)：一個強大到足以支持復雜事務(complextransactions)的協議在內部可能相當簡單，但那些復雜的事務可能會對協議的激勵機制產生復雜的系統影響，因為它們會以非常不正常的方式提議區塊。Verkle樹：Verkle樹確實有一些封裝復雜性，實際上比普通的Merkle哈希樹要復雜得多。然而，從系統上講，Verkle樹提供了與鍵值(key-value)映射完全相同的相對干凈和簡單的界面。主要的系統復雜性“泄漏”(leak)是攻擊者操縱Verkle樹使一個特定值有一個非常長的分支(branch)的可能性；但Verkle樹和Merkle樹的風險是相同的。我們如何權衡呢？

通常，封裝復雜性較低的選擇也是系統復雜性較低的選擇，因此有一個選擇顯然更簡單。但在其他時候，你必須在一種復雜性和另一種復雜性之間做出艱難的選擇。在這一點上應該清楚的是，如果是封裝復雜性，那么其危險性就會更低。一個系統復雜性帶來的風險不是一個簡單的規范長度的函數；規范中一個10行代碼的小片段與其他部分相互作用會比100行代碼的函數更復雜，否則就會被視為一個黑盒。然而，這種偏好封裝復雜性的方法存在局限性。任何一段代碼中都可能出現軟件bugs，當代碼越來越大時，出現錯誤的概率接近1。有時，當你需要以意想不到的新方式與子系統交互時，最初的封裝復雜性可能會變成系統復雜性。后者的一個例子是以太坊當前的兩級狀態樹(two-levelstatetree)，其特征是帳戶對象樹，其中每個帳戶對象依次有自己的存儲樹。

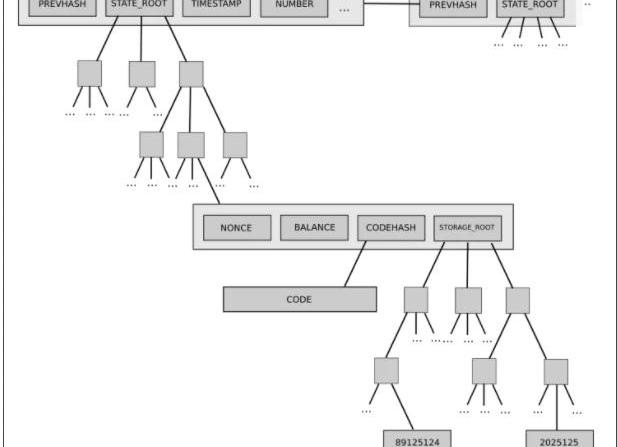
這個樹結構是復雜的，但在一開始，這種復雜性似乎被很好地封裝：協議的其余部分作為可讀寫的鍵/值存儲與樹交互，所以我們不必擔心樹是如何構造的。然而，后來，這種復雜性被證明具有系統性影響：帳戶擁有任意大的存儲樹的能力意味著沒有辦法可靠地期望某個特定的狀態部分(例如。“所有以0x1234開頭的帳戶”)具有可預測的大小。這使得將狀態分割成多個部分變得更加困難，使同步協議的設計和分布存儲進程的嘗試變得更加復雜。為什么封裝復雜性會變成系統性的？因為interface改變了。解決方法是什么？目前轉向Verkle樹的提議還包括轉向一個均衡的單層樹設計。最終，在任何給定的情況下，哪種類型的復雜性更受歡迎是一個沒有簡單答案的問題。我們所能做的最好的事情是適度地支持封裝復雜性，但不要太多，并在每個具體的情況下演練我們的判斷。有時候，犧牲一點系統復雜性來極大地降低封裝復雜性確實是最好的做法。其他時候，你甚至會誤判什么是封裝的，什么不是。每種情況都是不同的。

Tags：VITITAARKNARGravitySafuTitanoSHARK幣Mercenary

火幣下載