NOTE:必考知識點，CFA一級數量分析-常見概率分布-下_CFA

“人的一切痛苦，本質上都是對自己無能的憤怒。”

文：藍兔子讀難NOTES

圖：配圖來源于網絡

編碼：0008

因為篇幅的限制，我們上一篇文章只說了一半，在這一篇文章中，我們會繼續進行常見的概率分布內容的分享。可以說，在常見概率分布這一大章內容里面，最重要的內容就在接下來要說的里面，一個是正態分布(normaldistribution)，另一個是t分布(student‘st-distribution)，其也是掌握后面章節內容的關鍵知識點。

連續概率分布與正態分布

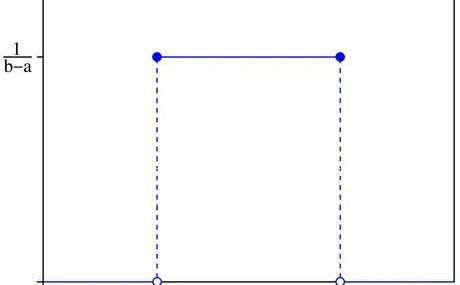
具體連續概率分布的定義我們在上一篇文章中已經進行過解釋，這里就不再贅述。我們直接來看一個連續均勻分布(continuousuniformdistribution)的PDF圖形：

Multicoin升任Spencer Applebaum和Shayon Sengupta為投資合伙人:金色財經報道，Multicoin官網宣布，投資團隊中任期最長的兩位成員Spencer Applebaum和Shayon Sengupta已晉升為投資合伙人。[2023/3/10 12:53:22]

因為每一個可能的結果發生的概率是相等的，所以其PDF曲線為一條水平線。這里需要強調說明一下，由于連續隨機變量可以有無數多個可能，因此針對某一確定的結果，我們近似的認為其發生的概率為0，因此在分析連續隨機變量相關問題時，我們應該取區間分析，而不能對點進行分析。

又因為任何一個隨機事件，其所有可能的結果的概率和為1，所以上圖中，該條直線的y軸坐標為1/(b-a)。當我們對區間(a，b)中任何一段子區間進行分析時，可以利用簡單的幾何原理算出相應的面積(概率)。

接下來，就是重中之重的正態分布，正態分布幾乎存在于我們生活的方方面面，無論是班上同學的考試成績，還是班上同學的身高體重，基本上都逃離不了正態分布的“上帝詛咒”，而且同一個目標對象的數量(樣本量)越是多，越是重復的厲害，那么就越正態。看看下面這兩幅圖，看看你是否能找到小正態的影子。

阿曼資本市場監管機構計劃建立虛擬資產監管框架:2月16日消息，阿曼金融市場監管機構阿曼資本市場管理局(Oman Capital Market Authority)表示，計劃建立一個虛擬資產框架，以“監管和發展阿曼蘇丹國的虛擬資產市場”。

根據監管機構的說法，該計劃有利于“積極發展阿曼數字資產和金融科技行業，創建虛擬資產監管框架將使監管機構能夠“為發行者和投資者提供替代融資和投資平臺，同時降低與該資產類別相關的風險。（news.bitcoin）[2023/2/16 12:11:27]

請別告訴我這是人為的，即便是人為的，為何偏偏就是這個樣子。那到底是哪個樣子呢，請看下圖：

正態分布雖然如上帝的“祝福”般占據了我們生活的方方面面，但是我們只需要把它當作一個工具即可，一把扳手，我們不需要知道它是怎么生產出來的，我們只需要了解他的一些性質即可：

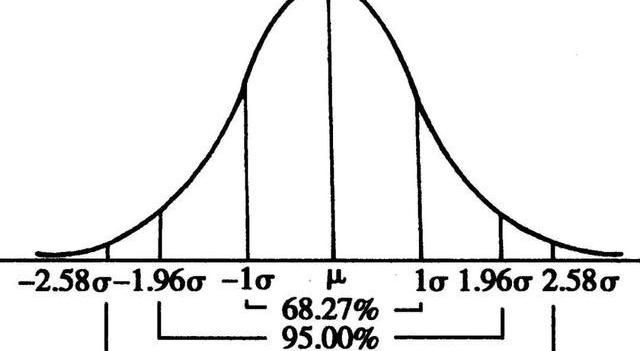
其PDF完全由均值和方差刻畫，通常記為N(均值，方差)；其圖形對稱，偏度為0，越中間概率越大，越兩端概率越小；如之前內容所講，正態分布的峰度為3，超額峰度為0；服從正態分布的隨機變量線性組合后還符合正態分布；標準正態分布概率區間幾個特殊值經常用要記住，如下圖(90%對應1.65個標準差，雖然圖中沒標，但也很重要)。

分析師認為Silvergate的股價不應該受FTX的影響:金色財經報道，在加密貨幣交易所FTX持續受到關注的情況下，Silvergate Capital（SI）在周二股價暴跌超過20%之后，受到了華爾街分析師的辯護。BTIG分析師Mark Palmer表示，他在周二與Silvergate的總裁Ben Reynolds進行了交談，后者告訴他Silvergate既不持有FTT代幣，也不針對它們進行貸款，FTX的挑戰對該公司沒有直接影響。另外，Canaccord強調，Silvergate自己不持有任何加密貨幣資產，應該能夠避免FTX情況帶來的額外風險。（coindesk）[2022/11/10 12:41:09]

接下來的內容是標準化的正態分布。如前文所言，正態分布表示為N(均值，方差)，盡管正態分布存在于我們生活的方方面面，但是這方方面面的正態分布卻也各不相同，且由于正態分布的PDF比較復雜，我們很難通過表達式去計算出其某區間的概率，更不可能給每一個參數不同的正態分布都列一個表格去查。

好在前輩們也糾結過這個問題，并且找到了解決方案：他們把標準正態分布的結果列成一張表，并提供一種把非標準正態分布轉換為標準正態分布的辦法，再拿這個分布去查表。

f2pool上線ETHW礦池:9月15日消息，f2pool已上線ETHW（EthereumPoW）礦池，并已將原ETH礦池遺留算力轉入ETHW挖礦。ETHW使用Ethash挖礦算法，支持GPU和Ethash ASIC礦機。[2022/9/15 6:59:19]

標準正態分布表示為N(0,1)，其中0為均值，1為方差，任何非標準正態分布都可以進行轉換，轉換后即可查標準正態分布的表得到相應的值。為了便于理解，舉個例子：

已知某公司股票的某參數符合正態分布，其均值為10，方差為9，即服從N(10，9)，問隨機抽取該股票參數中的某個值，該值小于5的概率，即F(5)。

雖然其服從正態分布，但不是標準正態分布，所以沒法直接查表，需要先進行轉換，轉換的方法就是：

(X-μ)/σ====即=====>>(5-10)/3

即查標準正態分布的F((5-10)/3)即可。

查表要注意，1、查表會不會，不會的同學看看書，這里就不解釋了；2、查得的是累積概率，可能需要再次進行換算。

標準正態分布也被稱為z分布或者u分布。

虧空風險(shortfallrisk)：指資產的收益低于最低可接受水平的概率，虧空風險是一個概率。這個最低可接受水平(shortfalllevel)用Rl表示。

持有10枚以上BTC的地址數量達到18個月高點:金色財經報道，Glassnode數據顯示，持有10枚以上BTC的地址數量達到18個月高點，數值為150,189。[2022/8/23 12:41:57]

羅伊的第一安全比例(Roy'ssafety-firstratio|SFration):

SFRatio=/標準差

從其公式上來看，第一安全比例代表的是每份超額風險所獲得的收益，這里的超額指的是投資收益相對于最低要求收益的超額。注意與夏普比率區分，夏普比率的超額是指投資收益相對于無風險收益超額。

同夏普比率一樣，每單位風險獲得的收益肯定是越多越好，所以怎么根據SFratio選擇組合你懂的。

對數正態分布與t分布

接下來是另一個非常重要的分布，學生t分布(studentt-distribution)，不要覺得名字奇怪，之所以叫這個名字，只是因為發表的人給自己取了個這么樣的筆名而已。就像正態分布也叫高斯分布一樣，只是名字而已。

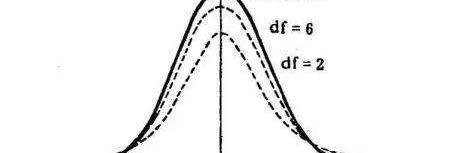
不過說到正態分布和t分布，他們不僅僅是名字都是發表者用的名字而已，他們還有很多的相似之處。怎么個相似法呢，先看圖：

我們之前說過，正態分布的樣本數量越多，就越正態分布。以考試成績為例，一個班50個同學的數據肯定沒有全校同學的數據那么“正態”。但是如果反過來，班上只有40個同學，或者只有10個同學，他們的成績還符合正態分布嗎？不難想象，當我們數據量越小時，越容易受到極端值的影響，當數據量太少時，就會和正態分布出現偏差。

我們有一位偉大的同學，叫做“Student”，同我們一樣，他也發現了這個現象，但是和我們不一樣的是，人家找到了小樣本的解決方案，后來被命名成t分布。t分布具有如下性質：

圖形如上圖所示，當自由度增大時，圖形逐步接近于正態分布；圖形完全由自由度(degreesoffreedom|df)刻畫；相比于正態分布，t分布圖形有低峰肥尾巴特質，因此峰度>3；這里說明一下，峰態雖然叫做“峰”態，但他看的不是峰有多高，而是尾巴有多肥。

下面是對數正態分布(lognormaldistribution)，雖然正態分布占據了我們生活的方方面面，但是他卻有一個問題：他的取值范圍在正負無窮的范圍內，而我們的資產，或者說股票的價格，不可能為負，所以導致其不能用于衡量資產的價格。因此，我們引入了對數正態分布(具體的過程比較有意思，但是這里不說)，如下圖：

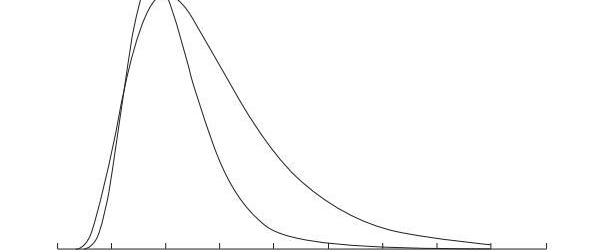
其有如下特點：

非負性，符合資產股票的價格定義域，偏度為正，所以一般用正態分布來衡量資產的風險，而用對數正態分布來衡量資產的價格。

最后還有一個知識點，叫做多元分布(multivariatedistribution)，這里大家不用詳細了解，只知道多元分布就像多元方程一樣，里面有多個元素。考試一般問你需要幾個參數才能刻畫出這個多元分布，只要記住以下內容就OK：

每一個元需要兩個參數來刻畫：一個均值，一個方差；每兩個元之間需要一個相關系數來刻畫，nC2；所以，假設有n元，需要的參數就是2*n+nC2，掏出你的計算器吧！

模擬

模擬就是通過事前對事情進行彩排，來預測和發現事情的發展方向，比如去面試前，你會進行一個模擬面試，考慮會有哪些問題，如何應對。

模擬有兩種，以面試為例，很多人都有面試過，自己可能也面試過多次，面試的常見套路，問題基本上就那些，你模擬的時候，你就能知道大概會問哪些問題，雖然每次面試不一樣，但是大差不差，你可以假設一種情景來分析，如果問這個問題怎么樣，如果問那個問題怎么樣。這就是蒙特卡羅模擬(MonteCarlosimulation)，我們也稱之為情景模擬，對解決如果咋的咋的(whatif)問題很有效。實際上，你就需要先假設這么一個如果(通常假設其符合某一分布)，但是其缺陷是，你一旦假設都錯了，那你就全盤皆輸。而且這種計算費電腦。

還有一個叫做歷史模擬(historicalsimulation)，就是根據歷史數據來模擬，比如搜集某個地方某一天過去100年的天氣情況來預測以后的天氣情況，由于其依賴歷史數據，所以不能進行情景分析，如果(whatif)氣象局搞了場人工降雨呢？而且時代在進步，萬事萬物都是在變，沒有什么是一成不變的，所以歷史模擬也存在問題。還有就是，你選的這段歷史數據萬一碰巧選到特殊的一段了，比如模擬經濟發展，你剛好選到二戰那一段呢？所以，我們通常進行樣本外測試(outofsampletest)，把數據拿到樣本外的歷史數據去試試，排除數據選擇問題(是那一段時間獨有的)。

兔紙的相關文章

CFA一級數量分析-貨幣的時間價值

CFA一級數量分析-數理統計基礎與收益

CFA一級數量分析-概率論基礎

Tags：PDFCFANOTEPDF幣PDF價格CFA幣CFA價格NOTE幣NOTE價格

狗狗幣最新價格