BOO:陸晨：論“猜”的重要性_Lattice

來源：金融界網站

作者：陸晨

數學競賽錯失“猜”出來的答案

初中二年級的時候，參加區里的數學競賽，在競賽中一路勢如破竹，凱歌高奏，很快就完成了其他所有的難題，只剩下最后一道難題了。我現在還記憶猶新，那次區里數學競賽的最后一道題是不定方程或者叫丟番圖方程。

從初中開始，我們就開始學習最簡單的一元一次方程，一個方程，一個未知數；后面陸續學了二元一次方程組，三元一次方程組。中學正規的教學內容給出的題目都是方程的個數和未知數的個數相同，這一要求，要等到上了大學，學習了高等數學中線性代數里的矩陣理論，特別是矩陣的秩以及線性獨立，線性相關等條件才恍然大悟，明白背后的原理。

未知數所代表的是人們感興趣的一些變量，每個方程代表了一個給定的關系。所以，一般的線性方程組的可解性要求是給定關系的數量要和未知數的數量相同。當所掌握的信息不完善，也就是，關系的數量少于未知數的數量時，這種特殊類型的方程就被稱之為不定方程或者丟番圖方程。丟番圖是公元3世紀希臘亞歷山大城的數學家，他曾對這些方程進行研究，并且是第一個將符號引入代數的數學家。

因為方程的個數少于未知數的個數，必須另辟蹊徑來完成方程式的求解，絕大多數的問題都是要找到整數解或者有理數解，數字性質的分析和邏輯推理在整個解題的過程中扮演著至關重要的角色，特別是整除和分解因子等。

中國小學生們非常熟悉的雞兔同籠問題就是一個家喻戶曉的不定方程問題。解題的方式就是實驗性的遍歷法，和電影中緊張刺激的開保險柜的場景是一樣的，要不停地去試和“猜”。

當時的最后一道競賽題就是一個普普通通的不定方程，而且，我當時看著題目，已經猜出來題目所要求的整數解，但是，作為一個初中二年級的學生，我幼稚地認為，“猜”出來的答案不能算“正式”的解答，所以，我就絞盡腦汁，想了各種方法想要“中規中矩”地把這道不定方程的題目解出來，但是，沒能成功，到交卷的鈴聲響起，我還是無法完成，心中無限懊惱。而且，我也沒有把自己“猜”出來的答案寫在考卷上，帶著遺憾的心情悻悻地離開了競賽的考場。

過了不久，競賽成績出來了，獲得了區里第二名，在發獎儀式上，我見到了那位也同樣是“猜”出了不定方程的正確答案，并把答案寫在考卷上的優勝女生。通過這個特殊的經歷，“猜”出數學問題的答案就永遠地銘刻在我的心里，同時，在那次初中數學競賽之后，因為好奇，想要知道怎樣才能解出不定方程，也開啟了我的數學探索之旅。

下面是一道簡單的不定方程題目，大家可以試一下：

觀點：灰度勝訴可能成為新牛市開始的催化劑:金色財經報道，CryptoSea匿名創始人Crypto Rover在社交媒體表示，法院裁定SEC拒絕Grayscale比特幣現貨ETF 的決定是錯誤的。下一步是什么？可能所有其他比特幣現貨 ETF 都會獲得批準，問題實際上是何時獲得批準，而不是是否獲得批準。該ETF是完全受監管的現貨ETF，而不是合成版本。現貨ETF意味著發行的每一股都必須以 1:1 的比例由實際比特幣支持。鑒于這一要求，我認為這可能成為新牛市開始的催化劑。[2023/8/30 13:04:38]

經過不斷的學習，我才知道，原來“猜”就是數學中的一種重要方法，在課堂中循規蹈矩所學習的演繹推理，都是象牙塔里被無限美化的游戲，當我們踏出“陽春白雪”的課堂，走進真實復雜殘酷的現實世界，面對的是數不勝數的信息不對稱性的挑戰，整個人生就是在不斷地解決一個又一個不定方程，充滿了不確定性。

“猜”出博士論文的無限維偏微分方程組的循環解

在中國我學習的是純數學，因為，我覺得純數學是最美的。一個腦筋急轉彎的問題就是：“請問，什么樣的圓最圓”，答案就是人頭腦想象中的圓最圓！因為，一旦把圓真實地畫出來，那種抽象的美好就被破壞掉了。

后來，出國留學，進入了庫朗數學研究所攻讀應用數學博士。在世界級頂尖高手如云的庫朗數學研究所的幾年，我不光學習了數學知識，也學習了新的哲學思想。對于數學和知識的看法發生了巨大的改變：一種知識是有用的，必須經過實際應用的檢驗，而不是在課堂里的自我陶醉。

眾所周之，數學是眾多科學中最嚴謹的一個分支，因為數學是建立在公理化的基礎之上，盡管在整個數學的發展過程中，遭遇了數次危機，但是，人類的智慧在每一次數學危機中被激發，創造出新的理論和方法，愈挫愈強，基礎更加堅實牢固。

讀數學博士的終極目標就是要完成博士論文，在數學上寫一篇博士畢業論文就是要研究一個全世界都沒有人碰過的問題，你是第一個來回答的。當面對這樣的未知問題的時候，過去，在課堂上的眾多學習方法，演繹，歸納，推理都無濟于事，也不可能有人會告訴你怎樣去解決面臨的難題。在這個場景下，唯一能夠幫助你砥礪向前的就是“猜”，要“猜”出正確答案，再來運用傳統的方法來加以證明。由此可見，整個完成論文的過程，“猜”的一步是最重要的，從0到1的飛躍！要想“猜”的正確，就需要兩樣東西：靈感和運氣。

我在庫朗數學研究所的導師是南非人PercyDeift教授，他為人嚴謹低調，一絲不茍，超級耐心的計算功力讓我嘆為觀止，欽佩不已，我們研究的是非線性偏微分方程中最神奇特殊的一部分：可積性微分系統，99％的微分方程是解不出來的，只能依靠計算數學中的數值逼近來了解微分方程解的性質。但是這一類鳳毛麟角的可積性偏微分方程竟然能夠寫出求解公式，這不得不算是上帝給人類的一個大禮包。但是，不要高興的太早，統治世界的量子力學第一基本原則：能量守恒定律表明，人類得到了一些，就必定要失去一些；對于可積性微分系統，盡管偏微分方程的解能夠寫出來，但是，求解公式中都是一些特殊函數，人們還是不得要領，必須依靠漸近分析和擾動理論來揭開最后的謎團發現那些“永恒存在”的非線性特征解。

Binance.US與MoonPay合作，允許用戶使用USDT買賣加密貨幣:金色財經報道，Binance.US發布公告稱，通過與MoonPay等第三方支付提供商合作，在Binance.US移動應用程序上推出增強版的“使用USDT購買和出售加密貨幣”功能，該功能允許用戶用美元為其USDT余額充值，然后使用USDT購買或出售平臺支持的150多種加密貨幣。為了更輕松地使用USDT為賬戶充值，MoonPay提供美元入金支持，支持使用借記卡、信用卡、Apple Pay和Google進行USDT購買支付。

彭博社曾報道稱，Binance.US發言人表示仍然有銀行合作伙伴允許該公司為客戶處理美元，但沒有透露具體名稱。[2023/8/23 18:16:13]

一個著名的可積性微分系統就是日本統計物理學家Toda戶田盛和在1967年發現的TodaLattice戶田晶格，是固態物理學中一維晶體的簡單模型。它是由一系列具有最鄰近相互作用的粒子鏈給出的，描述了哈密頓量

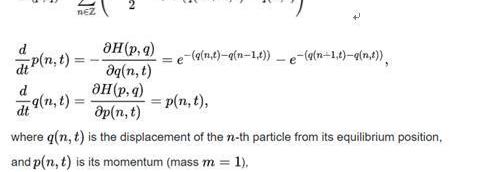
在全人類屈指可數的幾個可積性微分系統的光榮榜上，TodaLattice占有非常重要的地位，通過研究TodaLattice，讓人們進一步深入了解了非線性波的傳播過程。戶田晶格的微分方程的解可以被完全寫出來，是一組Soliton“孤立子”波！這又不得不稱為上帝賦予人類的另一個神奇的禮物，是只有在非線性的世界中才顯現的奇特現象。

蘇格蘭科學家、造船工程師約翰·史考特·羅素于1834年8月在英國格拉斯哥運河旁騎馬時在人類歷史上首次發現了自然界中的孤波——水面上滾動的水柱以每小時8-9英里的速度向前滾動，持續超過一英里。10年后，他在英國科學促進協會第14屆會議上，發表論文《論水波》也稱為羅素水波。后來，人們在其他幾個重要的科學領域都發現了神奇的“孤立子”波！

在準備博士論文的選題時，Deift教授給了我兩個題目，我忘記了第二個題目是什么，只記得第一篇是幾個日本的物理學家在戶田晶格的原有基礎上做出改進，在中間的晶格加了一個分叉，稱之為分叉的戶田晶格BranchedTodaLattice。他們做了一些計算機數值模擬，得到了一些有趣的非線性的性質。我的研究課題很簡單粗暴，就是要找到這個從負無窮到正無窮無限延申的分叉晶格上，非線性微分方程組的解。

拿到論文題目，我就開始著手深入研究，用Matlab做了大量的微分方程數值解的實驗，這個過程就是自然科學研究中著名的ControlledExperiment，控制實驗，不斷地從各個角度去嘗試，看看能夠得到什么樣的結果。

Circle金庫將超2.08億枚USDC轉入Coinbase:7月4日消息，據WhaleAlert監測，北京時間03:15:23，Circle金庫將超2.08億枚USDC（208,909,180枚）轉入Coinbase。[2023/7/4 22:16:42]

當時的計算機的運算能力非常有限，因為分叉的戶田晶格是個無窮維的非線性微分方程組，可以想見，運算量是多么巨大。每天晚上，我都伴隨著不斷發出聲響的計算機硬盤的“小夜曲”催眠進入夢鄉，第二天早上起來，檢查分析新的計算機數值模擬結果。

就這樣，很快的，一年就過去了，Deift教授開始不斷地催促我要加快研究的節奏，我也是心急如焚，希望能夠盡快有“質”的突破。

一個周末，我太太要去公司加班，我也和她一起坐從新澤西到紐約的PATH火車到了曼哈頓，她去中城的美國投行上班，我獨自一人回到庫朗數學研究所的辦公室繼續研究分叉的戶田晶格。午飯的時間到了，我在離辦公室不遠處的一家中餐館定了午餐，看看時間差不多了，我就從被稱為“紐約大學大門”的華盛頓廣場走過去，去取午餐。那天的天氣非常好，春光明媚，整個華盛頓廣場，行人、紐約大學的學生、游客絡繹不絕,熱鬧非凡。在廣場的中心就是每年紐約大學畢業典禮的主席臺所在地，一個巨大無比的有噴泉的水池，人們悠閑地坐在水池邊戲水交談，曬太陽，無比愜意。

我很快地取到了午飯，提著香噴噴的午飯往回走，當我再次經過那個人聲嘈雜的噴泉水池時，一個前所未有的靈感突然出現在我的腦海里，在那一刻我“猜”出來了這個無比復雜的無窮維非線性微分方程組的解，我想這樣試一下應該是正確的！一切都來的是那么突然和毫無準備，這大概就是靈感能夠產生的場景，經過無數次的苦思冥想，都無功而返，但是，在大腦中這些零零星星想法的種子都被保留下來，它們都在默默地等待最適合的那一刻，破土而出，大放光彩。

靈感，英文是Inspiration，在希臘語中指的是“神的靈氣”，根據網上詞典的解釋，靈感是一種罕見的在文藝、科技活動中瞬間產生的富有創造性的突發思維狀態，是學習過程中的巔峰狀態。

學習的目的不是為了好分數，為了好工作，為了考試，而是為了創造。創造就要有靈感，人的思維模式的最高境界就是靈感和悟性。而靈感和悟性和“猜”是緊密相連的。

我給各大商學院授課時，喜歡問企業CEO學員們一個問題：

人的心理年齡–人的生理年齡=？

答案是：悟性；人的心理年齡代表人所能理解的，而人的生理年齡代表人所實際所經歷的一切，悟性就是人不需要實際經歷而在認知的層面能夠理解通曉的，但那一部分不是科學，只有自己能夠很“模糊懵懂”的感覺到，無法用清晰的語言來向他人描述，做科學的說明和解釋。

早期買入SHIB和PEPE的3個聰明錢地址均獲利數百萬美元:金色財經報道，Lookonchain監測數據顯示，有3個聰明錢地址都在早期買入SHIB和PEPE，賺了數百萬美元。0x778c通過交易SHIB和PEPE分別賺了580萬美元、118萬美元。 0x2af8通過交易SHIB和PEPE分別賺了384萬美元、134萬美元。cryptopolitan.eth通過交易SHIB賺了245萬美元，通過交易PEPE賺了69.5萬美元。[2023/5/6 14:47:03]

在我“猜”出了微分方程組的解之后，剩下來的工作就是經過嚴格的數學推導和計算證明這個“猜”出來的答案是正確的。接下來的一個星期里，我足不出戶，天天就是不停地寫，把200多頁的論文計算一鼓作氣地完成了。現在回想起來，還是不勝須臾，感嘆“靈感”的偉大和神奇。Deift教授很高興我“猜”出來了這個當時未知的戶田晶格的微分方程的非線性循環解。

“猜”的方法在華爾街的投資交易中

拿到了應用數學博士之后，就隨著20世紀90年代后期轟轟烈烈的“上街”運動進軍美國的金融中心：華爾街。當時量化交易在華爾街剛剛興起不久，方興未艾。量化交易的特點就是要把人的主觀想法，也可以說是“猜”，還有情緒徹底從投資決策的過程中清理掉。用數學、統計、概率論來分析市場的變化，調整投資交易的結構和策略。一大批數學家、物理學家投身金融市場，信誓旦旦地要用數學來一統天下，替代人來交易。

經過了20多年華爾街的風風雨雨，特別是2000年的網絡泡沫、2001年的911、2008年的全球金融風暴，讓我認識到，當初這些單純的理科生的想法太幼稚了，數學是無法面對由復雜多變的人所構成的金融市場而運籌帷幄的。

金融無論是股票市場的交易還是信用市場的買賣都時時刻刻地反映出人的一個讓公理化的數學無法給出滿意答案的本性：后悔，在信用債券市場的違約就是“后悔”的表現！漸漸地,我發現，偉大的投資家索羅斯所總結是交易市場的真諦：數學不能控制金融市場,而心理因素才是控制市場的關鍵。

既然是人的心理對于金融市場起著決定作用，而且，很容易理解的，沒有人會告訴你他真實的心理活動。“猜”其他投資者的心理和想法就變得非常重要了。大家聽說過的英國著名經濟學家凱恩斯所提出的“選美理論”就是在金融市場中“猜”的方法的實際應用。

2017年諾貝爾經濟學獎獲得者，芝加哥大學行為經濟學教授理查德·泰勒RichardThaler在他的名著《Misbehaving》中就以“猜”為主題舉了一個發人深省的例子。

元宇宙平臺Roblox擬于2023下半年加入Meta Quest生態:1月10日消息，科技媒體The Verge稱，元宇宙平臺Roblox或擬于2023下半年加入Meta Quest生態，這意味著使用Quest VR頭顯設備的玩家可以進入Roblox元宇宙平臺。

實際上，去年五月就有傳言Roblox計劃進入VR市場，其首席執行官David Baszucki也暗示可能會推出配套的硬件VR設備，但目前可能會選擇與Meta合作。目前Meta已經確認將在2023年推出新款硬件設備Meta Quest 3，預計將在10月左右就行的Meta Connect大會上發布。（fossbytes）[2023/1/10 11:04:36]

“猜一個從0到100的數字，盡可能地讓這個數字接近其他所有人所想象的數字的平均值的2/3”。

這個例子非常有趣，它深刻地體現了思維的分層模式。最“笨”的第一層思維模式的人只能簡單地接收解讀表面的信息，既然是0到100之間的數字，那么大概率的可能就是“中間值”50。第二層思維模式的人，知道那些第一層思維模式的傻瓜一定會選50，那么他們更應該選50的2/3，即33.333作為答案；第三層思維模式的人知道第二層思維模式的人一定會選33.3333，那么，33.3333的2/3就應該是標準答案；第四層思維模式的人，通過推理分析，猜測，第三層模式的人一定會選22.2222，那么他們就應該選擇14.8！以此類推。

在原書中，泰勒給出的最終的博弈論中納什平衡的答案是0，因為每一高層級的思維方式所選的數字都要被2/3的權重所累，依次遞減，到最后博弈穩定狀態的只有最小的可選數字“0”。另外一個重要的方面就是要知道或者“猜”出來，在參與者中，第一層思維模式，第二層思維模式，第三層思維模式等等的人的比例，假設，有這兩方面所有的信息，那么，最后的“完美”答案就是第n層思維模式的人所選擇的數字和他們在全部參與者的比例的加權平均值！

Thaler在書中提到在1997年，他和金融時報FT一起搞了一次別開生面的“猜平均數”的大賽，面向所有的金融時報的讀者，大家都知道，金融時報和華爾街日報代表了全球金融報紙的最高水平，它的讀者大部分都是常青藤大學畢業的華爾街精英，聰明程度是首屈一指的。也就是說，在前面的分析中，第三層思維模式以上的人占比會非常大，最后的“猜測”的均值應該離數字0很接近。大賽揭曉的勝出的平均值數字是13，說明讀者里還是有相當比例的“傻瓜”，推高了大眾平均值的水平。

這個例子是對英國著名經濟學家，同時也是行為經濟學先驅的凱恩斯所提出的關于金融投資“選美理論”的一個社會實驗。另一個凱恩斯提出來的關于“猜”應用于金融市場的理論就是所謂的“動物精神”，指大多數投資者對于未來的市場變化一無所知，只能憑借自己的心情和感覺來“猜”，而并非經過傳統經濟學家們所說的冷靜理性地思考，被感情，情緒等心理因素所左右，深陷其中。

疫情中發現的用“猜”的方法解高階方程

時間快進到2020年，新冠病疫情期間，遵守政府頒布的居家隔離的防護措施，在家里和千千萬萬的民眾一起同心抗疫情。不經意間，重新撿起了我的老本行：數學研究。好好地補習了一下平面幾何中在正規課本中從沒有教過的十幾個稀奇古怪的定理，又做了幾套奧林匹克數學競賽題。其中遇到的一道解高階方程的題目，讓我重新體驗了“啊哈”的靈光乍現的感覺。我發現了一個用“猜”的方法來解高階方程的方法。不久后，又遇到一個類似的高階方程的題目，我再次施展新發現的“猜”的方法，駕輕就熟，一蹴而就，不免有些洋洋自得，準備把發現的“猜”的方法寫成論文來發表，讓更多的同學們在科技信息化高速發展的今天，利用更多的科技手段來提高經典傳統的數學的學習。這也是我最欣慰看到的。

21世紀，隨著科技的進步和發展，學生們每人都使用電腦來完成學習任務，計算機成為每個學生不可缺少的學習伙伴。計算機，顧名思義可以幫助人類快速準確地完成重復性的實驗和計算，但對于數學所依賴的邏輯思維還無法匹敵。在這里，我就介紹一下，所發現的利用計算機和Excel來快速地“猜”出解高階方程的根，再利用得到的結果分解高次多項式因子的方法。

給定方程：2=x^3+1

我們把方程展開變為：x^9+3x^6+3x^3-16x+9=0

觀察原來的初始方程，可以看出，x=1是一個解。

現在，我利用計算機和Excel，來“猜”一下這個高階方程的實數根。第一輪比較粗放的檢索，發現有一個實數根在-1.6和-1.7之間，見下圖，第一列為自變量x的數值，第二列為給定的9次多項式函數的值。

-1.2026.81417

-1.3027.08493

-1.4025.09556

-1.5018.60352

-1.603.924171

-1.70-24.7142

-1.80-76.0186

-1.90-162.727

再進行第二輪更為細致的搜索，對于-1.6的小數點后面幾位不斷試驗，觀察哪個取值使9次的多項式函數值趨近于0，得到-1.618034。

如果這個9次高階方程，除了1之外還有其他的實數根，那么根據對稱原理，這種實數根必定是成對出現的。因為給定的9次方程的首項系數為一，那么，不失一般性，可以假設有這樣的分解因子：x^2+Ax+B。根據一元二次方程的求根公式：這樣的一對根具有形式/2；C和D為整數，來自于原來多項式的各項系數。

那么，我們就來“猜”一下，哪個整數D可以使最后的小數表示是0.618.一個簡單的辦法就是試錯：√√5√7√11等等，對照一下便知。對于我來說，相對簡單一些，因為，當我看到結尾的0.618時，我就“猜”到結果了。0.618是著名的“黃金比例”的近似值，在數學、物理、社會、建筑以及人類的審美方面都起到了深刻的影響作用。

而黃金比例的精確值是/2,很容易，就可以得出/2應該是方程的一個實根。在Excel里把這個有根號表達式的計算結果作為自變量x的數值代入方程式，BOOM!,是對的。那么，馬上就得到另一個對稱的實數根就是黃金比例本身，多么美妙的數學！

原來的9次多項式可以分解為

x^9+3x^6+3x^3-16x+9=

余下的六次多項式的表達式為非負的多項式，因此，只有三對復數根！

不斷實驗和“猜”在找到第一個不等于1的實根的過程中起了決定性的作用。計算機從科技創新的角度引導古老經典的數學煥發出新的生命力。

另外一道是加拿大數學競賽題：x^2+x^2/〖〗^2=3

也用同樣的實驗和“猜”的方式快速地把它解出來。記F=x^2+x^2/〖〗^2；經過簡單的計算：F=1.25；F=44/9>3；那么，在區間中必定有一個實數解。用Excel做簡單的逼近發現1.618是近似的根。

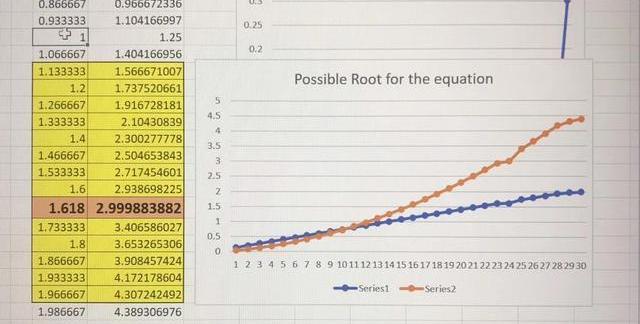
再把/2的數值代入表達式，在Excel里證實F/2）=3。那么另一個對稱的實根就是/2。

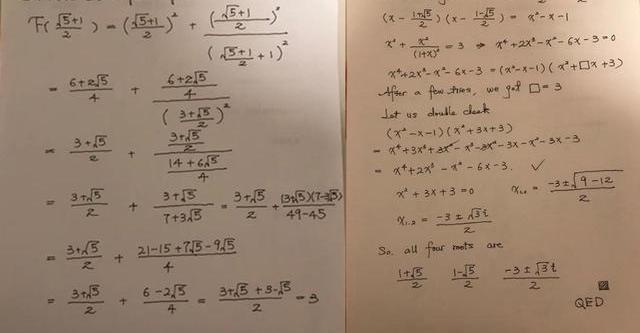
把原來的方程寫為標準的多項式的形式：x^4+2x^3-x^2-6x-3=；x^2+3x+3有復數根/2，/2。

下面的題出自于杜克數學大會：x^4-3x^3+3x+1=0

通過簡單地測試，可以看出在里有一個實根，在Excel里細細搜尋，很巧，又到了我們無比熟悉的區域1.6附近，果斷地代入黃金比例和它的孿生兄弟，證實兩個都是這個方程的實根，因為方程左面的表達式必可被分解，遂得到：

x^4-3x^3+3x+1=

這個方法利用計算機和Excel來發現事實，經過反復的實踐試錯，從觀察到的現象“猜”出深層的答案。當然，這背后有著嚴謹的分析論證做基礎，排除了眾多的不可能性，為最后認知的“跳躍”做好了準備和鋪墊。

結束語

在科學的圣殿中，就像我親身經歷的一樣，“猜”是一種非常重要的方法，特別是當面對一個完全未知的問題的時候，唯一的選擇就是要勇敢果斷幸運地“猜”出未來的正確的答案。

每個人走出象牙塔，進入令人眼花繚亂的真實世界的圍城，整個人生就像是開啟了一場“猜”的游戲。無論是在社會、工作、學習、生活中，還是在投資市場上，信息不對稱性的問題無處不在，“猜”就很自然地成為人生中的一部分：猜猜公司老板的想法，對自己的意見；猜猜談判桌上的交易對手的真實底牌，猜猜老師在期末考試里會出什么樣的難題，猜猜太太今年過生日喜歡什么禮物，猜猜追的精彩電視連續劇的結局，猜猜今年年底能不能晉升，不一而足。

當具有完備的信息時，決策是建立在對于所有可能出現場景的科學分析，風險評估之上。當所需的信息不完備的時候，人們就要開動自己的大腦“猜”出最好的可能的答案。

不可否認的，“猜”面臨著含有巨大的運氣成分，就是數學中的隨機性，那是人類無法控制和掌握的，但也正是這令人捉摸不定的隨機性讓我們的生活變得更加精彩和意想不到。

人生唯一確定的就是不確定性是永遠存在，那么就讓我們調整心態，不是躲閃或噤若寒蟬，而是主動擁抱不確定性，擁有更多的“反脆弱性”，讓整個人生更加精彩紛呈。

Tags：LatticeBOOPATHLattice幣是什么幣BOO幣BOO價格PATH價格PATH幣

聚幣