ING:零知識證明入門指南： 發展歷史、應用和基本原理_NAR

從頭梳理ZKP理論和應用層面的一些變化。撰文：HashKeyCapital

當前區塊鏈行業里零知識證明項目增速驚人，特別是ZKP在擴容和隱私保護兩個層面應用的崛起，令我們接觸到了各種花樣繁多的零知識證明項目。由于ZKP極富數學性的特質，對于加密愛好者來說，想要深度了解ZK的難度大幅提升。因此我們也希望從頭梳理ZKP理論和應用層面的一些變化，與讀者一起探索對于crypto行業的影響和價值——通過幾篇報告的形式共同學習，也作為HashKeyCapital研究團隊的思考總結。本篇是該系列的第一篇，主要介紹ZKP的發展歷史、應用和一些基本原理。

一、零知識證明的歷史

現代零知識證明體系最早來源于Goldwasser、Micali和Rackoff合作發表的論文：TheKnowledgeComplexityofInteractiveProofSystems，該論文提出于1985年，發表于1989年。這篇論文主要闡釋的是在一個交互系統中，經過K輪交互，需要多少知識被交換，從而證明一個證言是正確的。如果可以讓交換的知識為零，則被稱之為零知識證明。這里面會假設證明者具有無限資源，而驗證者只具有有限資源。而交互式系統的問題在于證明不完全是數學上可證的，而是概率意義上正確的，雖然概率很小(1/2^n)。

所以交互式系統并不完美，只有近似完備性，以此為基礎誕生的非交互式系統系統則具有完備性，成為零知識證明系統的完美所選。

早年的零知識證明系統在效率以及可用性方面都有所欠缺，所以一直都停留在理論層面，直到最近10年才開始蓬勃發展，伴隨著密碼學在crypto成為顯學，零知識證明走向臺前，成為至關重要的一個方向。特別是發展出一個通用的、非交互的、證明大小有限的零知識證明協議，是其中最關鍵的探索方向之一。

LayerZero USDC占Fantom生態中非多鏈USDC的75%以上:8月12日消息，LayerZero發推表示，Fantom上對LayerZero資產的支持正在不斷增長，LayerZero USDC目前占該生態系統中非多鏈USDC的75%以上，由超過16,000個獨立錢包持有。[2023/8/12 16:22:06]

基本上零知識證明就是要在證明的速度、驗證的速度和證明體積的大小之間做取舍，理想的協議是證明快、驗證快、證明體積小。

零知識證明最重要的突破是Groth在2010年的論文ShortPairing-basedNon-interactiveZero-KnowledgeArguments，也是ZKP里面最重要的一組zk-SNARK的理論先驅。

零知識證明在應用上最重要的進展就是2015年Z-cash使用的零知識證明系統，實現了對交易及金額隱私的保護，后來發展到zk-SNARK和智能合約相結合，zk-SNARK進入了更為廣泛的應用場景。

在此期間，一些重要的學術成果包括：

2013年的Pinocchio(PGHR13)：Pinocchio:NearlyPracticalVerifiableComputation，將證明和驗證時間壓縮到適用范圍，也是Zcash使用的基礎協議。

2016年的Groth16：OntheSizeofPairing-basedNon-interactiveArguments，精簡了證明的大小，并提升了驗證效率，是目前應用最多的ZK基礎算法。

Polygon聯創支持的NFT項目Pluto首個PFP系列“MISFITS”將于二季度發布:金色財經報道，Polygon聯合創始人兼首席執行官Sandeep Nailwal在社交媒體宣布，由其支持的NFT項目Pluto即將推出首個PFP系列“MISFITS”，預計會在2023年第二季度發布，但具體日期暫未公布。據悉，Pluto是Polygon Technology的NFT旗艦項目，旨在數字游戲世界中為用戶提供互動、有趣和創造性體驗，游戲合作完全由Polygon Technology通過旗下開發團隊與社區支持和元宇宙團隊提供支持，此外Pluto MISFITS還得到了Polygon Ventures的支持。[2023/5/30 11:47:58]

2017年的Bulletproofs(BBBPWM17)Bulletproofs:ShortProofsforConfidentialTransactionsandMore，提出了Bulletproof算法，非常短的非交互式零知識證明，不需要可信的設置，6個月以后應用于Monero，是非常快的理論到應用的結合。

2018年的zk-STARKs(BBHR18)Scalable,transparent,andpost-quantumsecurecomputationalintegrity，提出了不需要可信設置的ZK-STARK算法協議，這也是目前ZK發展另一個讓人矚目的方向，也以此為基礎誕生了StarkWare這個最重量級的ZK項目。

其他的發展包括PLONK、Halo2等也是極為重要的進展，也對zk-SNARK做出了某些層面上的改進。

Gemini：在Silvergate上沒有存放GUSD和客戶資金:金色財經報道，加密貨幣交易所Gemini在推特稱，正在積極監控Silvergate Bank情況，但在該銀行中沒有存放任何GUSD和客戶資金，此外該交易所已經停止通過ACH的客戶存款/提款，Silvergate Bank向Gemini發起的資金兌換服務也已暫停。[2023/3/3 12:39:45]

二、零知識證明的應用簡述

零知識證明最廣泛的兩個應用就是隱私保護和擴容。早期隨著隱私交易和幾個有名的項目Zcash和Monero等推出，隱私交易一度成為非常重要的門類，但由于隱私交易的必要性并沒有業界希望的那樣突出，因此這一類代表性項目開始慢慢進入二三線的陣營。而應用層面，擴容的必要性提升到無以復加，隨著以太坊2.0在2020年轉變為以rollup為中心的路線，ZK系列正式又回歸業界的視線，成為焦點。

隱私交易：隱私交易有很多已經實現的項目，包括使用SNARK的Zcash，Tornado,使用bulletproof的Monero,以及Dash。Dash嚴格意義上用的不是ZKP，而是一種簡單粗暴的混幣系統，只可以隱藏地址而不能隱藏金額，在此略過不表。

Zcash應用的zk-SNARKs交易步驟如下：

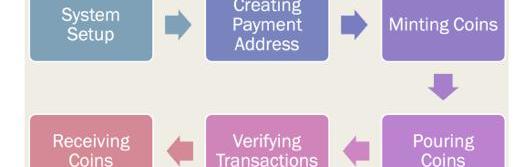
Source:DemystifyingtheRoleofzk-SNARKsinZcash

區塊鏈數據分析工具Dune引擎V2開始支持Avalanche數據:7月21日消息，區塊鏈數據分析工具Dune引擎V2開始支持Avalanche數據，目前上線的幾個儀表板包括Avalanche代幣供應量、Avalanche NFT市場和Snowsight（mempool流服務和用于Avalanche C鏈上最大可提取價值 MEV 搜索者的交易傳輸服務）。[2022/7/21 2:28:42]

Systemsetup階段生成證明秘鑰和驗證秘鑰，借助KeyGenfunction

CPA階段ECIES加密方法用來生成公鑰和私鑰

MintingCoins階段，生成新幣的數量。公共地址和幣的commitment

Pouring階段，生成zk-SNARK證明，證明被加到了pour交易賬本中

Verification階段，驗證者驗證Mint和Pour的交易量是否正確

Receiving階段，receiver接收幣。如果想使用收到的幣，則繼續調用Pouring，形成zk-SNARK驗證，重復上述4-6的步驟，完成交易。

Zcash使用零知識還是有局限性的，就是其基于UTXO,所以部分交易信息只是被shield了，而不是真正的掩蓋。因為其基于比特幣的設計的單獨網絡，所以難以擴展。真正使用shielding的使用率只有不到10%，說明隱私交易并沒有很成功的擴展。

Tornado使用的單一大混幣池更加通用，而且基于以太坊這樣“久經考驗”的網絡。Torndao本質上就是一個用了zk-SNARK的混幣池，可信設置基于Groth16的論文。TornadoCash可以提供的特性包括：

幣安將支持BEP2 THORChain（RUNE） 主網置換:6月4日，據官方公告，幣安將支持THORChain（RUNE）代幣從BEP2網絡置換到其主網。主網THORChain（RUNE）代幣的轉換將按照1:1的比例進行。幣安將于北京時間6月6日12:00暫停BEP2 RUNE代幣的充值、提現業務。[2022/6/4 4:02:17]

只有被存進去的coin可以被提取

沒有幣可以被提取兩次

證明過程和幣的廢止通知是綁定的，相同證明但不同Nullifier的哈希不會允許提幣

安全性有126-bit的安全，不會因為composition而降級

Vitalik提到過，和擴容相比，隱私相對比較容易實現，如果一些擴容的protocol都可以成立的話，隱私基本上不會成為問題。

擴容：ZK的擴容可以在一層網絡上做，如Mina，也可以在二層網絡上做，即zk-rollup.ZKrollup的思路可能最早來自于Vitalik于2018的post，On-chainscalingtopotentially~500tx/secthroughmasstxvalidation。

ZK-rollup有兩類角色，一類是Sequencer,還有一個是Aggregator。Sequencer負責打包交易，Aggregator負責將大量的交易合并并創造一個rollup,并形成一個SNARK證明，這個證明會和Layer1以前的狀態進行比較，進而更新以太坊的Merkle樹，計算新的狀態樹。

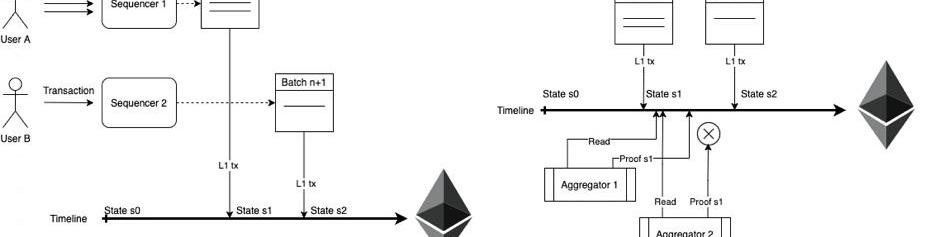
Source:Polygon

ZKrollup的優缺點：

優點：費用低，不像OP會被經濟攻擊，不需要延遲交易，可以保護隱私，快速達成最終性

缺點：形成ZK證明需要大計算量，安全問題，不抗量子攻擊，交易順序可能被改變

Source:以太坊research

根據數據可用性以及證明的方法，Starkware對L2有一張經典的分類圖：

Source:Starkware

目前市場上最有競爭力的ZKrollup項目有：Starkware的StarkNet，Matterlabs的zkSync和Aztec的Aztecconnect，Polygon的Hermez和Miden，Loopring，Scroll等。

基本上技術路線就在于SNARK(及其改進版本)和STARK的選擇，以及對EVM的支持。

Aztec開發了通用化的SNARK協議-Plonk協議，運行中的Aztec3可能會支持EVM，但是隱私優先于EVM兼容

Starnet用的是zk-STARK，一種不需要可信設置的zkp，但是目前不支持EVM，有自己的編譯器和開發語言

zkSync也是用的plonk，支持EVM。zkSync2.0是EVM兼容的，有自己的zkEVM

Scroll，一種EVM兼容的ZKrollup,團隊也是以太坊基金會zkEVM項目的重要貢獻者

簡要討論下EVM兼容性問題：

ZK系統和EVM的兼容一直令人頭疼，一般項目會在兩者間取舍。強調ZK的可能會在自己的系統里做一個虛擬機，并有自己的ZK語言以及編譯器，但會加重開發者的學習難度，而且因為基本上不開源，會變成一個黑箱子。一般業界目前是兩種選擇，一是和Solidity的操作碼完全兼容，另一種是設計一種新的虛擬機同時ZK友好并兼容Solidity。業界一開始也沒有想到可以這么快的融合，但是近一兩年技術的快速迭代，讓EVM的兼容提升到一個新高度，開發者可以做到一定程度的無縫遷移，是振奮人心的進展，這將影響ZK的開發生態和競爭格局。我們會在之后的報告中仔細討論這個問題。

三、ZKSNARK實現的基本原理

Goldwasser、Micali和Rackoff提出了零知識證明有三個性質：

完整性：每一個擁有合理見證的聲明，都是可以被驗證者驗證的

可靠性：每一個只擁有不合理見證的聲明，都不應該被驗證者驗證

零知識：驗證過程是零知識的

所以為了了解ZKP,我們從zk-SNARK開始，因為很多目前的區塊鏈應用都是從SNARK開始。首先，我們先了解一下zk-SNARK。

zk-SNARK的意思是：零知識證明是zero-knowledgeSuccintNon-interactiveARgumentsofKnowledge。

ZeroKnowledge：證明過程零知識，不會暴露多余信息

Succinct：驗證體積小

Non-interactive：非交互過程

ARguments：計算具備可靠性，即有限計算能力的證明者不能偽造證明，無限計算能力的證明者可以偽造證明

ofKnowledge：證明者無法在不知道有效信息的情況下構建出一個參數和證明

對于證明者來說，在不知道證據的情況下，構造出一組參數和證明是不可能的。

Groth16的zk-SNARK的證明原理和如下：

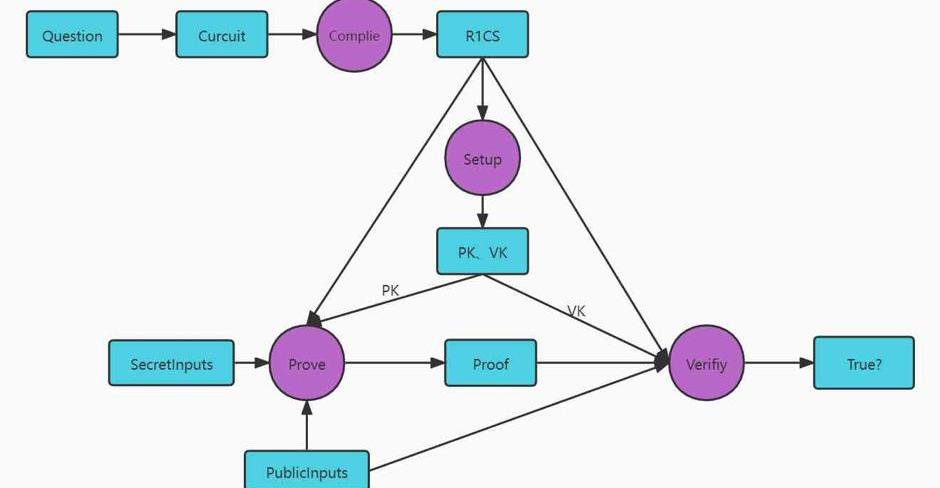
Source：https://learnblockchain.cn/article/3220

步驟是：

將問題轉換為電路

將電路拍平成R1CS的形式.

R1CS轉換成QAP形式

建立trustedsetup,生成隨機參數，包括PK(provingkey)，VK(verifyingkey)

zk-SNARK的證明生成和驗證

下一篇我們將開始研究zk-SNARK的原理、應用，通過幾個案例來透視ZK-SNARK的發展，并探索它與zk-STARK的關系等。

來源：金色財經

Tags：ARKNARASHINGMarko FinanceINARIKakashi SenseiBORING

世界幣